题目内容
【题目】如图,已知一次函数y1=![]() x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣
x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣![]() ,0).
,0).
(1)求二次函数的最大值;
(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程![]() =0的根,求a的值;
=0的根,求a的值;
(3)若点F、G在图象C′上,长度为![]() 的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.

【答案】(1)5;(2)![]() ;(3)P(
;(3)P(![]() ,0)
,0)
【解析】试题分析: (1)首先利用待定系数法求出二次函数解析式,然后求出其最大值;
(2)联立y1与y2,求出点C的坐标为C(![]() ,
, ![]() ),因此使y2>y1成立的x的取值范围为0<x<
),因此使y2>y1成立的x的取值范围为0<x<![]() ,得s=1+2+3=6;将s的值代入分式方程,求出a的值;
,得s=1+2+3=6;将s的值代入分式方程,求出a的值;
(3)如图,四边形DEFG是一个梯形,将其面积用含有未知数的代数式表示出来,这个代数式是一个二次函数,根据其最值求出未知数的值,进而得到面积最大时点D、E的坐标.
试题解析:
解:(1)∵二次函数y2=﹣x2+mx+b经过点B(0,1)与A(2﹣![]() ,0),
,0),
∴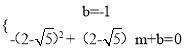 ,
,
解得![]() ,
,
∴l:y1=![]() x+1;
x+1;
C′:y2=﹣x2+4x+1.
∵y2=﹣x2+4x+1=﹣(x﹣2)2+5,
∴ymax=5;
(2)联立y1与y2得: ![]() x+1=﹣x2+4x+1,解得x=0或x=
x+1=﹣x2+4x+1,解得x=0或x=![]() ,
,
当x=![]() 时,y1=
时,y1=![]() ×
×![]() +1=
+1=![]() ,
,
∴C(![]() ,
, ![]() ).
).
使y2>y1成立的x的取值范围为0<x<![]() ,
,
∴s=1+2+3=6.
代入方程得![]() ,
,
解得a=![]() ;
;
经检验a=![]() 是分式方程的解.
是分式方程的解.
(3)∵点D、E在直线l:y1=![]() x+1上,
x+1上,
∴设D(p, ![]() p+1),E(q,
p+1),E(q, ![]() q+1),其中q>p>0.
q+1),其中q>p>0.
如答图1,过点E作EH⊥DG于点H,则EH=q﹣p,DH=![]() (q﹣p).
(q﹣p).
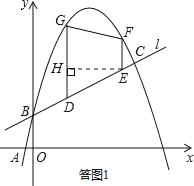
在Rt△DEH中,由勾股定理得:EH2+DH2=DE2,即(q﹣p)2+[![]() (q﹣p)]2=(
(q﹣p)]2=(![]() )2,
)2,
解得q﹣p=2,即q=p+2.
∴EH=2,E(p+2, ![]() p+2).
p+2).
当x=p时,y2=﹣p2+4p+1,
∴G(p,﹣p2+4p+1),
∴DG=(﹣p2+4p+1)﹣(![]() p+1)=﹣p2+
p+1)=﹣p2+![]() p;
p;
当x=p+2时,y2=﹣(p+2)2+4(p+2)+1=﹣p2+5,
∴F(p+2,﹣p2+5),
∴EF=(﹣p2+5)﹣(![]() p+2)=﹣p2﹣
p+2)=﹣p2﹣![]() p+3.
p+3.
S四边形DEFG=![]() (DG+EF)EH=
(DG+EF)EH=![]() [(﹣p2+
[(﹣p2+![]() p)+(﹣p2﹣
p)+(﹣p2﹣![]() p+3)]×2=﹣2p2+3p+3
p+3)]×2=﹣2p2+3p+3
∴当p=![]() 时,四边形DEFG的面积取得最大值,
时,四边形DEFG的面积取得最大值,
∴D(![]() ,
, ![]() )、E(
)、E(![]() ,
, ![]() ).
).
如答图2所示,过点D关于x轴的对称点D′,则D′(![]() ,﹣
,﹣![]() );
);

连接D′E,交x轴于点P,PD+PE=PD′+PE=D′E,
由两点之间线段最短可知,此时PD+PE最小.
设直线D′E的解析式为:y=kx+b,
则有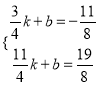 ,
,
解得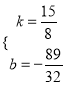
∴直线D′E的解析式为:y=![]() x﹣
x﹣![]() .
.
令y=0,得x=![]() ,
,
∴P(![]() ,0).
,0).
点睛: 本题是二次函数压轴题,综合考查了二次函数与一次函数的图象与性质、待定系数法、函数最值、分式方程的解、勾股定理、轴对称最短路线等知识点,涉及考点众多,难度较大.本题难点在于第(3)问,涉及两个最值问题,第1个最值问题利用二次函数解决,第2个最值问题利用几何性质解决.

 名校课堂系列答案
名校课堂系列答案