题目内容
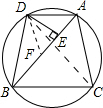
如图，已知圆内接△ABC中，AB＞AC，D为
的中点，DE⊥AB于E，求证：BD2-AD2=AB•AC．
 |
| BAC |
证明：在BA上截取BF=CA，连DF，DC，如图，
∵D为
的中点，
∴DB=DC，
又∵∠DBF=∠ACD，
∴△DBF≌△DCA，
∴DF=DA，
而DE⊥AB，
∴AE=EF，
∴BF=BE-EF=BE-AE=CA，
又∵BD2=BE2+DE2，AD2=AE2+DE2，
∴BD2-AD2=BE2-AE2=（BE+AE）（BE-AE）=AB•AC，即证．
∵D为
|
| BAC |
∴DB=DC，
又∵∠DBF=∠ACD，
∴△DBF≌△DCA，
∴DF=DA，
而DE⊥AB，
∴AE=EF，
∴BF=BE-EF=BE-AE=CA，
又∵BD2=BE2+DE2，AD2=AE2+DE2，
∴BD2-AD2=BE2-AE2=（BE+AE）（BE-AE）=AB•AC，即证．
练习册系列答案
相关题目
延长CO交⊙O于点D，连接AD．
