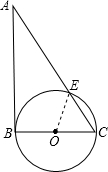
题目内容
△ABC中，∠B=90°，以BC为直径作圆交AC于E，若BC=12，AB=12
，则
的度数为（ ）
| 3 |
 |
| BE |
| A．60° | B．80° | C．100° | D．120° |
连OE，如图，
∵∠B=90°，BC=12，AB=12
，
∴AC=
=24，
∴BC=
AC．
∴∠A=30°，∠C=60°，
由BC为⊙O直径，
∴OE=OC，
∴△OEC是等边三角形
∴∠BOE=2∠C=2×60°=120°，
∴
的度数为120°．
故选D．
∵∠B=90°，BC=12，AB=12
| 3 |
∴AC=
122+(12
|
∴BC=
| 1 |
| 2 |
∴∠A=30°，∠C=60°，
由BC为⊙O直径，
∴OE=OC，
∴△OEC是等边三角形
∴∠BOE=2∠C=2×60°=120°，
∴
|
| BE |
故选D．
练习册系列答案
期末集结号系列答案
相关题目
