Question

【题目】在等腰△ABC中，AB＝AC，BC＝4，⊙O是△ABC的外接圆，若⊙O的半径为4，则△ABC的面积为_____．

Answer 1

【答案】12或4

【解析】

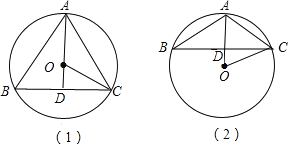
如图（1）和（2），由等腰三角形的外心在三角形的底边的高上，根据勾股定理求出OD的长，进一步求出BD的长，根据三角形的面积公式即可求出答案．

解：连接OA交BC于D，连接OC，

∵圆O是等腰三角形的外接圆，O是外心，

∴AD⊥BC，BD＝DC＝BC＝2，有两种情况：

（1）如图（1）：

∵OC＝4，由勾股定理得：

OD＝＝＝2，

即：AD＝4+2＝6，

∴S△ABC＝BCAD＝×4×6＝12；

（2）如图（2）：同理可求OD＝2，

AD＝4﹣2＝2，

∴S△ABC＝BCAD＝×4×2＝4；

故答案为：12或4．