Question

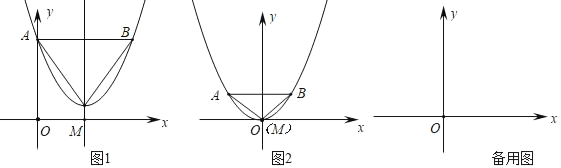
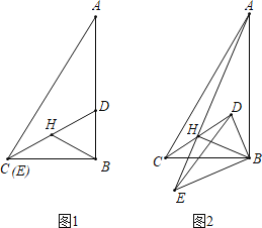
【题目】 问题发现：如图（1）在Rt△ABC和Rt△BDE中，∠A=∠DEB=30°，BC=BE=6，Rt△BDE绕点B逆时针旋转，H为CD的中点，当点C与点E重台时，BH与AE的位置关系为______，BH与AE的数量关系为______；

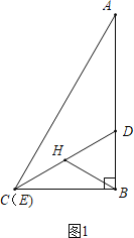
问题证明：在Rt△BDE绕点B旋转的过程中，（1）中的结论是否仍然成立？若成立，请就图（2）的情形给出证明若不成立，请说明理由；

拓展应用：在Rt△BDE绕点B旋转的过程中，当DE∥BC时，请直接写出BH2的长．

Answer 1

【答案】问题发现：AE⊥BH，AE=2BH；问题证明：（1）中结论成立，证明详见解析；拓展应用：12+3或12-3

【解析】

问题发现：如图1中，结论：AE=2BH，AE⊥BH．解直角三角形求出AC，BH即可判断．

问题证明：如图2中，（1）中结论成立．延长BH到F使得HF=BH，连接CF．设AE交BF于O．证明△ABE∽△BCF即可解决问题．

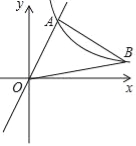
拓展应用：分两种情形：①如图3-1中，当DE在BC的下方时，延长AB交DE于F．②当DE在BC的上方时，利用上面结论求出AE2即可解决问题．

解：问题发现：如图1中，结论：AE=2BH，AE⊥BH．

理由：在Rt△ABC中，∵BC=6，∠A=30°，

∴AE=2BC=12，

在Rt△CDB中，∵∠DCB=30°，

∴CD==4，

∵CH=DH，

∴BH=CD=2，

∴==2，

∴AE=2BH．

故答案为AE⊥BH，AE=2BH．

问题证明：如图2中，（1）中结论成立．

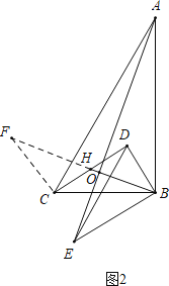
理由：延长BH到F使得HF=BH，连接CF．设AE交BF于O．

∵CH=DH，BH=HF，∠CHF=∠BHD，

∴△CHF≌△DHB（SAS），

∴BD=CF，∠F=∠DBH，

∴CF∥BD，

∵AB=BC，BE=BD，

∴BE=CF，

∴==，

∵CF∥BD，

∴∠BCF+∠CBD=180°，

∵∠ABC+∠DBE=∠ABD+∠CBD+∠CBD+∠CBE=∠CBD+∠ABE=180°，

∴∠BCF=∠ABE，

∴△ABE∽△BCF，

∴∠CBF=∠BAE，==，

∴AE=BF=2BH，

∵∠CBF+∠ABF=90°，

∴∠ABF+∠BAE=90°，

∴∠AOB=90°，

∴BH⊥AE．

拓展应用：如图3-1中，当DE在BC的下方时，延长AB交DE于F．

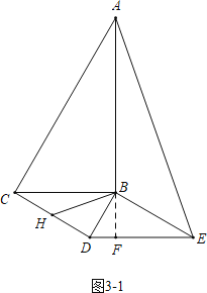
∵DE∥BC

∴∠ABC=∠BFD=90°，

由题意BC=BE=6，AB=6，BD=2，DE=4，

∵BDBE=DEBF，

∴BF==3，

∴EF=BF=3，

∴AF=6+3，

∴AE2=AF2+EF2=（6+3）2+（3）2=144+36．

∵AE=2BH，

∴AE2=12BH2，

∴BH2=12+3

如图3-2中，当DE在BC的上方时，同法可得AF=6-3，EF=3，

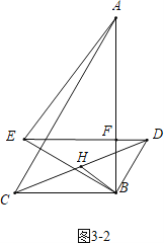
∴BH2==（=12-3．