题目内容
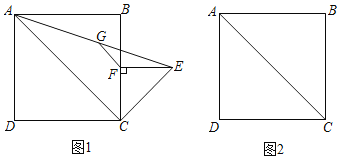
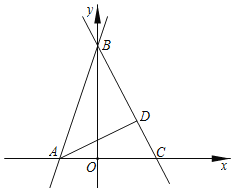
【题目】如图,在等腰△ABC中,AB=AC,tan∠CAB=![]() ,AD=AB,AH⊥BD于点H,连接CD交AH于点E,连接BE,BE=
,AD=AB,AH⊥BD于点H,连接CD交AH于点E,连接BE,BE=![]() ,则BD的长为_____.
,则BD的长为_____.

【答案】4![]() .
.
【解析】
过点C作CF⊥AB于F,由三角函数得出tan∠CAB=![]() ,设CF=4a,AF=3a,由勾股定理得出AC=5a,得出BF=AB﹣AF=2a,由勾股定理得出BC=
,设CF=4a,AF=3a,由勾股定理得出AC=5a,得出BF=AB﹣AF=2a,由勾股定理得出BC=![]() =2
=2![]() a,得出sin∠CBF=
a,得出sin∠CBF=![]() ,证出点BD关于AH对称,AC=AD,DH=BH,得出∠ABD=∠ADB,∠ABE=∠ADE,∠DEH=∠BEH,∠ADC=∠ACD,得出∠ACD=∠ABE,证出A、E、B、C四点共圆,由圆周角定理得出∠ABC=∠AEC,证出∠CBF=∠BEH,得出sin∠BEH=
,证出点BD关于AH对称,AC=AD,DH=BH,得出∠ABD=∠ADB,∠ABE=∠ADE,∠DEH=∠BEH,∠ADC=∠ACD,得出∠ACD=∠ABE,证出A、E、B、C四点共圆,由圆周角定理得出∠ABC=∠AEC,证出∠CBF=∠BEH,得出sin∠BEH=![]() ,即可得出答案.
,即可得出答案.
解:过点C作CF⊥AB于F,如图所示:
∴tan∠CAB=![]() ,
,
设CF=4a,AF=3a,
AC=![]() =5a,
=5a,
∵AB=AC,
∴BF=AB﹣AF=5a﹣3a=2a,
在Rt△BDF中,
BC=![]() =2
=2![]() a,
a,
∴sin∠CBF=![]() ,
,
∵AB=AD,AH⊥BD,
∴点BD关于AH对称,AC=AD,DH=BH,
∴∠ABD=∠ADB,∠ABE=∠ADE,∠DEH=∠BEH,∠ADC=∠ACD,
∴∠ACD=∠ABE,
∴A、E、B、C四点共圆,
∴∠ABC=∠AEC,
∵∠AEC=∠DEH,∠DEH=∠BEH,
∴∠ABC=∠BEH,即∠CBF=∠BEH,
∴sin∠BEH=![]() ,
,
∵BE=![]() ,
,
∴![]() ,
,
∴BH=2![]() ,
,
∴BD=2BH=4![]() ,
,
故答案为:4![]() .
.

练习册系列答案
相关题目