题目内容
【题目】夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元.
（1）设第
天生产空调
台，直接写出与之间的函数解析式，并写出自变量的取值范围.
（2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第天的利润为
元，试求与
之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少.
【答案】（1）y=40+2x（1≤x≤10）；（2）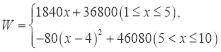
，第5天，46000元.
【解析】
试题分析：（1）根据接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，直接得出生产这批空调的时间为x天，与每天生产的空调为y台之间的函数关系式；
（2）根据基本等量关系：利润=（每台空调订购价﹣每台空调成本价﹣增加的其他费用）×生产量即可得出答案．
试题解析：（1）∵接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，
∴由题意可得出，第x天生产空调y台，y与x之间的函数解析式为：y=40+2x（1≤x≤10）；
（2）当1≤x≤5时，W=（2920﹣2000）×（40+2x）=1840x+36800，
∵1840＞0，∴W随x的增大而增大，
∴当x=5时，W最大值=1840×5+36800=46000；
当5＜x≤10时，
W=[2920﹣2000﹣20（40+2x﹣50）]×（40+2x）=﹣80（x﹣4）2+46080，
此时函数图象开口向下，在对称轴右侧，W随着x的增大而减小，又天数x为整数，
∴当x=6时，W最大值=45760元．
∵46000＞45760，
∴当x=5时，W最大，且W最大值=46000元．
综上所述：．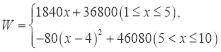
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
【题目】行驶中的汽车，在刹车后由于惯性的作用，还要向前方滑行一段距离才能停止，这段距离称为“刹车距离”，为了测定某种型号的汽车的刹车性能(车速不超过140 km/h)，对这种汽车进行测试，测得数据如下表：
刹车时车速/km·h－1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)以车速为x轴，以刹车距离为y轴，建立平面直角坐标系，根据上表对应值作出函数的大致图象；
(2)观察图象．估计函数的类型，并确定一个满足这些数据的函数解析式；
(3)该型号汽车在国道发生了一次交通事故，现场测得刹车距离为46.5 m，推测刹车时的车速是多少？请问事故发生时，汽车是超速行驶还是正常行驶？
