题目内容
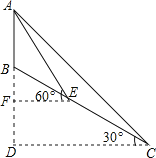
【题目】如图,重庆欢乐谷的摩天轮是西南地区最高的摩天轮,号称“重庆之限”.摩天轮是一个圆形,直径AB垂直水平地面于点C,最低点B离地面的距离BC为1.6米.某天,妈妈带着洋洋来坐摩天轮,当她站在点D仰着头看见摩天轮的圆心时,仰角为37,为了选择更佳角度为洋洋拍照,妈妈后退了49米到达点D’,当洋洋坐的桥厢F与圆心O在同一水平线时,他俯头看见妈妈的眼睛,此时俯角为42,已知妈妈的眼睛到地面的距离为1.6米,妈妈两次所处的位置与摩天轮在同一平面上,则该摩天轮最高点A离地面的距离AC约是( )
(参考数据:sin37≈0.60,tan37≈0.75,sin42≈0.67,tan42≈0.90)
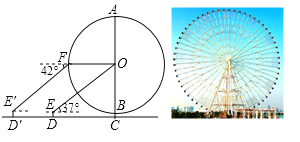
A.118.8米B.127.6米C.134.4米D.140.2米
【答案】B
【解析】
连接EB,根据已知条件得到E′,E,B在同一条直线上,且E′B⊥AC,过F做FH⊥BE于H,则四边形BOFH是正方形,求得BH=FH=OB,设AO=OB=r,解直角三角形即可得到结论.
解:连接EB,
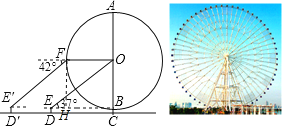
∵D′E′=DE=BC=1.6
∴E′,E,B在同一条直线上,且E′B⊥AC,
过F做FH⊥BE于H,
则四边形BOFH是正方形,
∴BH=FH=OB,
设AO=OB=r,
∴FH=BH=r,
∵∠OEB=37°,
∴tan37°=![]() ,
,
∴BE=![]() ,
,
∴EH=BD-BH=![]() ,
,
∵EE′=DD′=49,
∴E′H=49+![]() ,
,
∵∠FE′H=42°,
∴tan42°=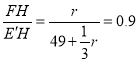 ,
,
解得r≈63,
∴AC=2×63+1.6=127.6米,
故选:B.

练习册系列答案
相关题目