题目内容
两条平行直线被第三条直线所截,内错角的平分线( )
| A.互相重合 | B.互相平行 | C.相交 | D.互相垂直 |
B
分析:首先由AB∥CD,根据两直线平行,内错角相等,得出∠ABC=∠BCD,再由BE,CF分别是∠ABC,∠BCD的角的平分线,根据角平分线的定义,得出∠ABC=2∠2,∠BCD=2∠3,从而∠2=∠3,最后根据内错角相等,两直线平行,得出BE∥CF.

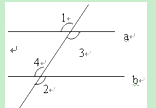
如图,AB∥CD,BE,CF分别是∠ABC,∠BCD的角的平分线,
∵AB∥CD,
∴∠ABC=∠BCD,
∵BE,CF分别是∠ABC,∠BCD的角的平分线,
∴∠ABC=2∠2,∠BCD=2∠3,
∴∠2=∠3,
∴BE∥CF.
故选B
点评:本题是平行线的判定和平行线的性质的应用,初学者容易混淆二者的区别.通过解答本题,意在帮助同学们正确认识二者的区别和联系.

如图,AB∥CD,BE,CF分别是∠ABC,∠BCD的角的平分线,
∵AB∥CD,
∴∠ABC=∠BCD,
∵BE,CF分别是∠ABC,∠BCD的角的平分线,
∴∠ABC=2∠2,∠BCD=2∠3,
∴∠2=∠3,
∴BE∥CF.
故选B
点评:本题是平行线的判定和平行线的性质的应用,初学者容易混淆二者的区别.通过解答本题,意在帮助同学们正确认识二者的区别和联系.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

 ABD
ABD
 ∠2=
∠2=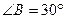 ,
,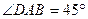 .
.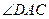 的度数;
的度数;
 ,∠C=45°+3
,∠C=45°+3