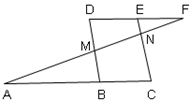
题目内容
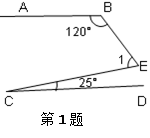
如图，∠C=45°，∠B=45°+2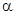
，∠C=45°+3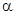，AE平分∠BAD，则∠CAE= ；
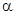，∠C=45°+3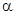，AE平分∠BAD，则∠CAE= ；126°
首先运用三角形内角和定理求出α的度数，从而得出∠BAC的度数，然后根据角平分线的性质，求出∠EAB的度数，进而得出∠CAE的度数．
解：在△ABC中：
∵∠BAC+∠B+∠C=180°（三角形内角和是180°），
∴45°+45°+2α+45°+3α=180°，
∴5α=180°-135°=45°，
∴α=9°，
∴∠BAC=45°+3α=45°+27°=72°，
∴∠DAB=180°-72°=108°，
∵AE平分∠BAD，
∴∠EAB=54°，
∴∠CAE=∠EAB+∠BAC=54°+72°=126°．
故答案为：126°．
解：在△ABC中：
∵∠BAC+∠B+∠C=180°（三角形内角和是180°），
∴45°+45°+2α+45°+3α=180°，
∴5α=180°-135°=45°，
∴α=9°，
∴∠BAC=45°+3α=45°+27°=72°，
∴∠DAB=180°-72°=108°，
∵AE平分∠BAD，
∴∠EAB=54°，
∴∠CAE=∠EAB+∠BAC=54°+72°=126°．
故答案为：126°．
练习册系列答案
相关题目
