题目内容
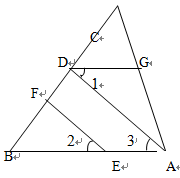
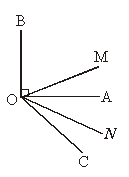
如图，已知∠BDE=∠DEF，∠DFE=∠B，试说明：∠CFD+∠C=180°
解：∵∠BDE=∠DEF（已知），
∴ ∥ ( )
∴∠DFE=∠ADF ( )
∵∠DFE=∠B（已知）
∴∠ADF=∠B
∴ ∥ ( )
∴∠CFD+∠C=180°（ ）
解：∵∠BDE=∠DEF（已知），
∴ ∥ ( )
∴∠DFE=∠ADF ( )
∵∠DFE=∠B（已知）
∴∠ADF=∠B
∴ ∥ ( )
∴∠CFD+∠C=180°（ ）
，
)
）
）
)
）
）
解：∵∠BDE=∠DEF（已知）
∴ AB ∥ EF (内错角相等，两直线平行)
∴∠DFE=∠ADF ( 两直线平行 ，内错角相等)
∵∠DFE=∠B（已知）
∴∠ADF=∠B
∴ DF ∥ BC ( 同位角相等，两直线平行)
∴∠CFD+∠C=180°（两直线平行，同旁内角互补）
考查的是平行线的判定与性质，熟知平行线的判定与性质的区别是解答此题的关键，即性质与判定的已知和结论正好相反，都是角的关系与平行线相关
∴ AB ∥ EF (内错角相等，两直线平行)
∴∠DFE=∠ADF ( 两直线平行 ，内错角相等)
∵∠DFE=∠B（已知）
∴∠ADF=∠B
∴ DF ∥ BC ( 同位角相等，两直线平行)
∴∠CFD+∠C=180°（两直线平行，同旁内角互补）
考查的是平行线的判定与性质，熟知平行线的判定与性质的区别是解答此题的关键，即性质与判定的已知和结论正好相反，都是角的关系与平行线相关
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
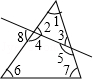
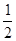∠AOC
∠AOC
