Question

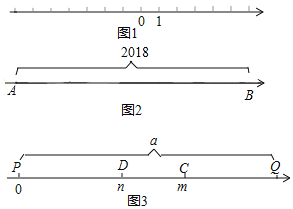
【题目】已知在纸面上有一数轴（如图1），折叠纸面．

（1）若1表示的点与﹣1表示的点重合，则﹣4表示的点与　 　表示的点重合；

（2）若﹣2表示的点与8表示的点重合，回答以下问题：

①16表示的点与　 　表示的点重合；

②如图2，若数轴上A、B两点之间的距离为2018（A在B的左侧），且A、B两点经折叠后重合，则A、B两点表示的数分别是　 　、　 　．

（3）如图3，若m和n表示的点C和点D经折叠后重合，（m＞n＞0），现数轴上P、Q两点之间的距离为a（P在Q的左侧），且P、Q两点经折叠后重合，求P、Q两点表示的数分别是多少？（用含m，n，a的代数式表示）

Answer 1

【答案】（1）4；（2）①-10；②﹣1006、1012；（3）点P表示的数为：；点Q表示的数为：

【解析】

（1）由表示1与﹣1的两点重合，利用对称性即可得到结果；

（2）由﹣2表示的点与8表示的点重合，确定出3为对称点，得出两项的结果即可；

（3）根据（2）的计算方法进行解答．

（1）若1表示的点与﹣1表示的点重合，则原点为对称点，所以﹣4表示的点与4表示的点重合；

（2）由题意得：（﹣2+8）÷2＝3，即3为对称点，

①根据题意得：2×3﹣16＝﹣10；

②∵3为对称点，A、B两点之间的距离为2018（A在B的左侧），且A、B两点经折叠后重合，

∴A表示的数＝﹣+3＝﹣1006，B点表示的数＝+3＝1012；

（3）点P表示的数为：；点Q表示的数为：．

故答案为：（1）4；（2）①﹣10； ②﹣1006，1012．（3）点P表示的数为：；点Q表示的数为：．