题目内容
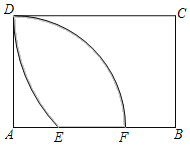
【题目】如图，以矩形ABCD的顶点A为圆心，线段AD长为半径画弧，交AB边于F点；再以顶点C为圆心，线段CD长为半径画弧，交AB边于点E，若AD＝
，CD＝2，则DE、DF和EF围成的阴影部分面积是_____．
【答案】2π+2﹣4
【解析】
如图，连接EC．首先证明△BEC是等腰直角三角形，根据S阴=S矩形ABCD-（S矩形ABCD-S扇形ADF）-（S矩形ABCD-S扇形CDE-S△EBC）=S扇形ADF+S扇形CDE+S△EBC-S矩形ABCD计算即可．
如图，连接EC．
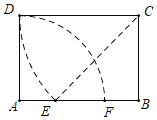
∵四边形ABCD是矩形，
∴AD＝BC＝2，CD＝AB＝EC＝2，∠B＝∠A＝∠DCB＝90°，
∴BE＝
＝
＝2，
∴BC＝BE＝2，
∴∠BEC＝∠BCE＝45°，
∴∠ECD＝45°，
∴S阴＝S矩形ABCD﹣（S矩形ABCD﹣S扇形ADF）﹣（S矩形ABCD﹣S扇形CDE﹣S△EBC）
＝S扇形ADF+S扇形CDE+S△EBC﹣S矩形ABCD
＝
+
×2×2﹣2×2，
＝2π+2﹣4．
故答案为：2π+2﹣4．
练习册系列答案
相关题目
