题目内容
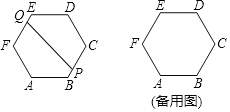
【题目】一个边长为60米的正六边形跑道,P、Q两人同时从A处开始沿相反方向都跑一圈后停止,P以4米/秒逆时针方向、Q以5米/秒顺时针方向,PQ的距离为d米,设跑步时间为x秒,令d2=y,
(1)跑道全长为 米,经过 秒两人第一次相遇.
(2)当P在BC上,Q在EF上时,求y关于x的函数解析式;并求相遇前当x为多少时,他们之间的距离最大.
(3)直接写出P、Q在整个运动过程中距离最大时的x的值及最大的距离.
【答案】(1)360,40;(2)当x=24时,d的最大值为12![]() 米;(3)PQ的最大值为120米.
米;(3)PQ的最大值为120米.
【解析】
(1)由正六边形的性质可得跑道全长;根据相遇时P、Q两人的路程之和等于跑道全长列出方程,即可求解;
(2)如图,连接BF,过点Q作QH⊥BC于H,可证四边形FBHQ是矩形,可得QH=BF,而FB易求,则QH可得,显然PH就是Q跑x秒的路程减去P跑x秒的路程,于是PH可得,再由勾股定理即可求出y关于x的函数解析式,然后根据二次函数的性质求解即可;
(3)根据正六边形的性质可知:点A,B,C,D,E,F在以AD中点为圆心,AB长为半径的圆上,则可得当PQ为直径时,PQ的值最大,据此解答即可.
解:(1)∵六边形ABCDEF是正六边形,∴AB=BC=CD=DE=EF=AF=60米,
∴跑道全长=6×60=360米,
∴4x+5x=360,∴x=40s,即经过 40秒两人第一次相遇.
故答案为:360,40;
(2)∵六边形ABCDEF是正六边形,∴∠A=∠F=∠B=120°,
如图,连接BF,过点Q作QH⊥BC于H,
∵∠A=120°,AB=AF=60米,∴∠AFB=∠ABF=30°,BF=60![]() 米,
米,
∴∠BFE=∠FBC=90°,∴四边形FBHQ是矩形,
∴QH=BF=60![]() 米,FQ=BH,
米,FQ=BH,
∵AF+FQ=5x米,AB+BP=4x米,∴PH=x米,
∴y=QP2=PH2+QH2,
∴y=x2+10800,(15≤x≤24)
∴当x=24时,d的最大值为12![]() 米;
米;

(3)∵六边形ABCDEF是正六边形,∴点A,B,C,D,E,F在以AD中点为圆心,AB长为半径的圆上,
∵当x=60s时,5×60=300米,则点Q与点B重合,4×60=240米,则点P与点E重合,
∴BE为直径时,如图,P、Q之间的距离最大,
∵六边形ABCDEF是正六边形,∴BE=2AB=120米,即PQ的最大值为120米.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案