题目内容
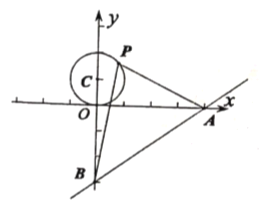
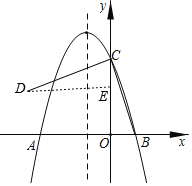
【题目】如图,已知抛物线y=﹣x2+bx+3的对称轴为直线x=﹣1,分别与x轴交于点A,B(A在B的左侧),与y轴交于点C.
(1)求b的值;
(2)若将线段BC绕点C顺时针旋转90°得到线段CD,问:点D在该抛物线上吗?请说明理由.
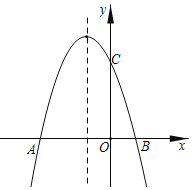
【答案】(1)b=﹣2;(2)点D不在该抛物线上,见解析
【解析】
(1)根据抛物线的对称轴公式,可求出b的值,
(2)确定函数关系式,进而求出与x轴、y轴的交点坐标,由旋转可得全等三角形,进而求出点D的坐标,代入关系式验证即可.
解:(1)∵抛物线y=﹣x2+bx+3的对称轴为直线x=﹣1,
∴![]() =﹣1,
=﹣1,
∴b=﹣2;
(2)当x=0时,y=3,因此点C(0,3),即OC=3,
当y=0时,即﹣x2+bx+3=0,解得x1=﹣3,x2=1,因此OB=1,OA=3,
如图,过点D作DE⊥y轴,垂足为E,由旋转得,CB=CD,∠BCD=90°,
∵∠OBC+∠BCO=90°=∠BCO+∠ECD,
∴∠OBC=∠ECD,
∴△BOC≌△CDE (AAS),
∴OB=CE=1,OC=DE=3,
∴D(﹣3,2)
当x=﹣3时,y=﹣9+6+3=0≠2,
∴点D不在该抛物线上.

练习册系列答案
相关题目