题目内容
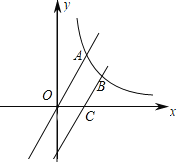
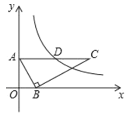
【题目】已知:如图,在平面直角坐标系xoy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
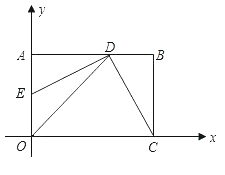
(1)填空:写出点D、E的坐标:D,E.
(2)求过点E、D、C的抛物线的解析式;
(3)点G的坐标为(1,0),在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)D(2,2),E(0,1);(2)![]() ;(3)存在三个满足条件的点Q,使得△PCG是等腰三角形,
;(3)存在三个满足条件的点Q,使得△PCG是等腰三角形,![]() 或
或![]() 或
或![]()
【解析】
(1)根据OA=2,OC=3,OD平分∠AOC,可得D点坐标,根据三角形全等可求得E点坐标;
(2)已知三点,可用待定系数法求出二次函数解析式;
(3)应当明确△PCG构成等腰三角形有三种情况,逐一讨论求解,要求思维的完备性.
(1)∵OA=2,OC=3,OD平分∠AOC,
∴AD=OA=2,∴D(2,2),
∵DE⊥DC,∴∠ADE+∠BDC=90°,
∵∠BCD+∠BDC=90°,
∴∠ADE =∠BCD ,
在Rt△ADE和Rt△BCD中,
∠A=∠B=90°,AD=BC=2,∠ADE =∠BCD ,
∴△ADE≌△BCD,∴AE=BD=1,
∴OE=1,即E(0,1).
(2)设过点E、D、C的抛物线的解析式为![]() ,
,

把C(3,0)、D(2,2)、E(0,1)三点坐标代入解析式中得:
 解得
解得 ,
,
故过点E、D、C的抛物线的解析式为![]() ,
,
(3)设P(t,2),又G(1,0),C(3,0)
∴![]() ,
,![]() ,GC=2,
,GC=2,
有三种情况,分别讨论:
①PG=PC,则![]() ,解得t=2.
,解得t=2.
∴P(2,2),此时点Q与点P重合,即Q(2,2);
②若PG=GC,则![]() ,解得t=1,
,解得t=1,
∴P(1,2),此时GP⊥x轴,GP与该抛物线在第一象限内的交点Q的横坐标为1,
代入抛物线解析式可得Q(1,![]() );
);
③若PC=GC,则![]() ,解得t=3
,解得t=3
∴P(3,2),此时PC=GC=2,PCG是等腰直角三角形,
过点Q作QH⊥x轴于点H,
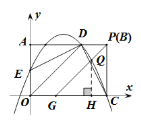
则QH=GH,设QH=h,即Q(h+1,h)
∴![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴Q(![]() ).
).
综上所述,存在三个满足条件的点Q,使得△PCG是等腰三角形,
分别是:![]() 或
或![]() 或
或![]() .
.

【题目】“新型冠状病毒肺炎”疫情牵动着亿万国人的心,为进一步加强疫情防控工作,兰州市某学校利用网络平台进行疫情防控知识测试.洪涛同学对九年级1班和2班全体学生的测试成绩数据进行了收集、整理和分析,研究过程中的部分数据如下.
信息一:疫情防控知识测试题共10道题目,每小题10分;
信息二:两个班级的人数均为40人;
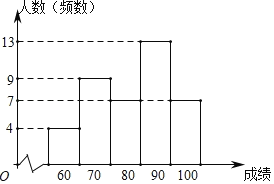
信息三:九年级1班成绩频数分布直方图如图,
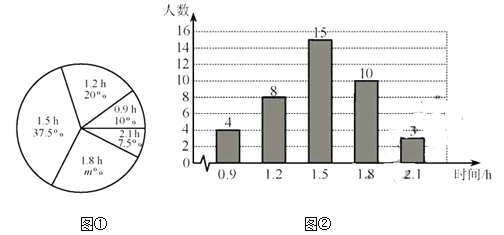
信息四:九年级2班平均分的计算过程如下,
![]() 80.5(分);
80.5(分);
信息五:
统计量 班级 | 平均数 | 中位数 | 众数 | 方差 |
九年级1班 | 82.5 | m | 90 | 158.75 |
九年级2班 | 80.5 | 75 | n | 174.75 |
根据以上信息,解决下列问题:
(1)m= ,n= ;
(2)你认为哪个班级的成绩更加稳定?请说明理由;
(3)在本次测试中,九年级1班甲同学和九年级2班乙同学的成绩均为80分,你认为两人在各自班级中谁的成绩排名更靠前?请说明理由.