题目内容
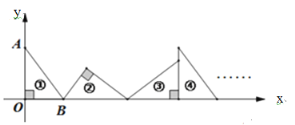
【题目】如图,在平面直角坐标系中,Rt△ABO的直角顶点O在原点,AO在y轴上,BO在x轴上,且AO=4,BO=3,△ABO绕着各顶点向x轴正方向连续翻滚(始终保持一条边在x轴上)得到多个三角形,请问第2020个三角形的直角顶点坐标为_________________.
【答案】(8076,0)
【解析】
利用勾股定理求出AB的长,先根据图形求出第3个三角形的直角顶点的坐标.观察图形不难发现,每3个三角形为一个循环组依次循环,用2020除以3,根据商和余数的情况确定出第2020个三角形的直角顶点到原点O的距离,然后写出坐标即可.
解:∵AO=4,BO=3,
∴AB=![]() =5,
=5,
∴第3个三角形的直角顶点坐标为:(12,0).
∵2020÷3=673…1,
∴第2020个三角形是第674组的第一个直角三角形,其直角顶点与第673组的最后一个直角三角形顶点重合,
∵673×12=8076,
∴第2020个三角形的直角顶点的坐标是(8076,0).
故答案为:(8076,0).

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目