题目内容
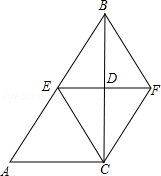
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

| A.BC=AC | B.CF⊥BF | C.BD=DF | D.AC=BF |
D
试题分析:∵EF垂直平分BC,∴BE=EC,BF=CF。
∵CF=BE,∴BE=EC=CF=BF。∴四边形BECF是菱形。
当BC=AC时,∠ACB=90°,∠A=45°,∴∠EBC=45°。∴∠EBF=2∠EBC=2×45°=90°。∴菱形BECF是正方形。故选项A不符合题意。
当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项B不符合题意。
当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项C不符合题意。
当AC=BD时,无法得出菱形BECF是正方形,故选项D符合题意。
故选D。

练习册系列答案
相关题目







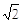 ,过点A作AE⊥AC,AE=1,连接BE,则tanE=
,过点A作AE⊥AC,AE=1,连接BE,则tanE=