题目内容
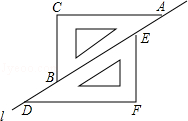
（2013年四川南充3分）如图，正方形ABCD的边长为2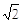
，过点A作AE⊥AC,AE=1，连接BE，则tanE=
_.
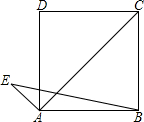
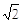，过点A作AE⊥AC,AE=1，连接BE，则tanE=_.
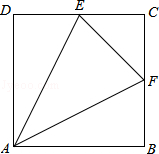
。如图，延长CA使AF=AE，连接BF，过B点作BG⊥AC，垂足为G，
∵四边形ABCD是正方形，∴∠CAB=45°。∴∠BAF=135°。
∵AE⊥AC，∴∠BAE=135°。∴∠BAF=∠BAE。
∵在△BAF和△BAE中，
，∴△BAF≌△BAE（SAS）。
∴∠E=∠F。
∵四边形ABCD是正方形，BG⊥AC，∴G是AC的中点。∴BG=AG=2。
在Rt△BGF中，
，即tanE=。
∵四边形ABCD是正方形，∴∠CAB=45°。∴∠BAF=135°。
∵AE⊥AC，∴∠BAE=135°。∴∠BAF=∠BAE。
∵在△BAF和△BAE中，
，∴△BAF≌△BAE（SAS）。∴∠E=∠F。
∵四边形ABCD是正方形，BG⊥AC，∴G是AC的中点。∴BG=AG=2。
在Rt△BGF中，
，即tanE=。
练习册系列答案
相关题目
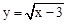的自变量x的取值范围是x＞3 
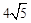，BC=4，向矩形ABCD外作△CDE，使△CDE为等腰三角形，且点E在边BC所在的直线上，请你画出图形，直接写出OE的长，并画出体现解法的辅助线．