题目内容
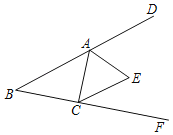
【题目】△ABC在平面直角坐标系中的位置如图所示：
（1）写出点A，B，C三点的坐标；
（2）若△ABC各顶点的横坐标不变，纵坐标都乘以﹣1，请你在同一坐标系中描出对应的点A'，B'，C'，并依次连接这三点，所得的△A'B'C'与原△ABC的位置关系是什么？
（3）在x轴上作出一点P，使得AP平分∠BAC．（保留作图痕迹，不写作法）
【答案】（1）A(3，4)B(1，2)C(5，1)；（2）作图见解析，△A'B'C'与△ABC关于x轴对称；（3）作图见解析．
【解析】
（1）根据A，B，C的位置写出坐标即可．
（2）首先写出A'，B'，C'的坐标，作出△A'B'C'即可．
（3）利用尺规作∠BAC的平分线交x轴于P，射线AP即为所求．
（1）A(3，4)B(1，2)C(5，1)．
（2）如图，△A'B'C'即为所求，△A'B'C'与△ABC关于x轴对称．
（3）如图，射线AP即为所求．
练习册系列答案
相关题目
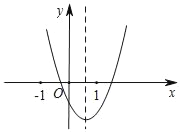
【题目】小颖根据学习函数的经验，对函数
的图象与性质进行了探究，下面是小颖的探究过程，请你补充完整．
（1）列表：
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | -2 | -1 | 0 | 1 | 0 | -1 | k | … |
①
____；
②若
，
，
，为该函数图象上不同的两点，则
____；
（2）描点并画出该函数的图象；
（3）①根据函数图象可得：该函数的最大值为____；
②观察函数的图象，写出该图象的两条性质________________________；_____________________；
③已知直线
与函数的图象相交，则当
时，
的取值范围为是____．
