Question

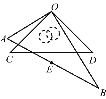
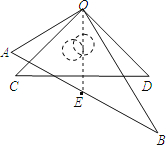
【题目】将一副三角板按如图所示的方式叠放在一起,两直角顶点重合于点O.

(1)求∠AOD+∠BOC的度数;

(2)当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数.

Answer 1

【答案】(1)∠AOD+∠BOC=180°；(2)∠AOC=15°.

【解析】

（1）再根据直角三角板的性质可直接得出结论；

（2）连接OE，根据OE是CD的中垂线可知∠COE=45°，再由E是AB的中点可知OE=AB=AE，故可得出∠AOE=∠A=60°，再根据∠AOC=∠AOE-∠COE即可得出结论．

（1）∵∠BOC=∠AOB+∠COD-∠AOD，

∴∠AOD+∠BOC=∠AOB+∠COD=90°+90°=180°；

（2）连接OE，

∵OE是CD的中垂线，

∴∠COE=45°．

又∵E是AB的中点，

∴OE=AB=AE，．

∴∠AOE=∠A=60°，

∴∠AOC=∠AOE-∠COE=15°．