Question

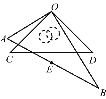
【题目】如图⊙O是△ABC的外接圆，圆心O在这个三角形的高AD上，AB=10，BC=12，求⊙O的半径．

Answer 1

【答案】解：如图，连接OB．

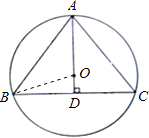
∵AD是△ABC的高．

∴BD= BC=6

在Rt△ABD中，AD= = =8．

设圆的半径是R．

则OD=8﹣R．

在Rt△OBD中，根据勾股定理可以得到：R2=36+（8﹣R）2

解得：R= ．

【解析】连接OB，根据垂经定理求出BD的长，在Rt△ABD中由勾股定理求得AD=8，设圆的半径是R，则OD=8-R，在Rt△OBD中由勾股定理可求得R的值.解答此题的关键是作出辅助线OB.注意：垂径定理和勾股定理常常在一起中应用.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能正确解答此题．