Question

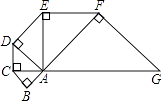
【题目】已知四边形ABCD是正方形，F是边AB，BC上一动点，DE⊥DF，且DE＝DF，M为EF的中点．

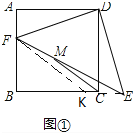
(1)当点F在边AB上时(如图①)．

①求证：点E在直线BC上；

②若BF＝2，则MC的长为多少．

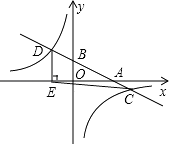
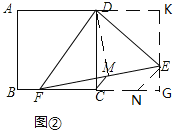
(2)当点F在BC上时(如图②)，求的值．

Answer 1

【答案】(1)①证明见解析；②；(2) .

【解析】

（1）①连接CE，证明△ADF≌△CDE，得到∠DCE=∠DAF=90°即可；

②作FK∥MC，证明CM=FK，求出FK=BF即可；

（2）过点E作CD的平行线分别交AD、BC的延长线于K、Q，EN∥MC，根据平行线等分线段定理即可解答．

(1)①证明：如图①，连接CE.

∵DE⊥DF，∴∠FDE＝90°.

∵四边形ABCD是正方形，

∴∠ADC＝∠DAF＝∠DCB＝90°，

DA＝DC.

∴∠ADC－∠FDC＝∠FDE－∠FDC，

即∠ADF＝∠CDE.

又∵DF＝DE，

∴△DAF≌△DCE(SAS)．

∴∠DAF＝∠DCE＝90°，

∴∠DCE＋∠DCB＝180°.

∴点E在直线BC上．

②如图①，作FK∥MC，∵M为EF的中点，

∴CM=FK，

∵∠DMB=∠DCB=90°，

∴D、M、C、B四点共圆，

∴∠MCD=∠MBD=45°，

∴∠BKF=45°，

∵BF=2，∴FK=2，

∴CM=FK=；

(2) 过点E作CD的平行线分别交AD、BC的延长线于K、G，EN∥MC，

∵M为EF的中点，

∴CM=NE，FC=CN，

∴NG=EG=BF，

．