题目内容
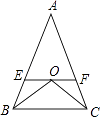
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

【答案】(1)CE=AF;证明见解析;(2)135°;(3)![]() .
.
【解析】试题分析: (1)由正方形额等腰直角三角形的性质判断出△ADF≌△CDE即可;
(2)设DE=k,表示出AE,CE,EF,判断出△AEF为直角三角形,即可求出∠AED;
(3)由AB∥CD,得出![]() ,求出DM,DO,再判断出△DFN∽△DCO,得到
,求出DM,DO,再判断出△DFN∽△DCO,得到![]() ,求出DN即可.
,求出DN即可.
试题解析:
(1)CE=AF;
证明:在正方形ABCD,等腰直角三角形CEF中,
FD=DE,CD=CA,∠ADC=∠EDF=90°
∴∠ADF=∠CDE,
∴△ADF≌△CDE,
∴CE=AF,
(2)设DE=k,
∵DE:AE:CE=1: ![]() :3
:3
∴AE=![]() k,CE=AF=3k,
k,CE=AF=3k,
∴EF=![]() k,
k,
∵AE2+EF2=7k2+2k2=9k2,AF2=9k2,
即AE2+EF2=AF2
∴△AEF为直角三角形,
∴∠BEF=90°
∴∠AED=∠AEF+DEF=90°+45°=135°;
(3)∵M是AB中点,
∴MA=![]() AB=
AB=![]() AD,
AD,
∵AB∥CD,
∴![]() ,
,
在Rt△DAM中,DM=![]() ,
,
∴DO=![]() ,
,
∵OF=![]() ,
,
∴DF=![]() ,
,
∵∠DFN=∠DCO=45°,∠FDN=∠CDO,
∴△DFN∽△DCO,
∴![]() ,
,
∴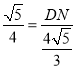 ,
,
∴DN=![]() ,
,
∴CN=CD-DN=4-![]() =
=![]() .
.

练习册系列答案
相关题目