题目内容
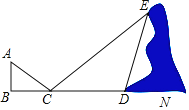
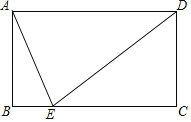
【题目】如图,已知矩形ABCD中,BC=2AB,点E在BC边上,连接DE、AE,若EA平分∠BED,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过点A作AF⊥DE于F,根据角平分线上的点到角的两边距离相等可得AF=AB,利用全等三角形的判定和性质以及矩形的性质解答即可.
解:如图,过点A作AF⊥DE于F,
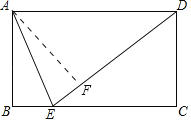
在矩形ABCD中,AB=CD,
∵AE平分∠BED,
∴AF=AB,
∵BC=2AB,
∴BC=2AF,
∴∠ADF=30°,
在△AFD与△DCE中
∵∠C=∠AFD=90°,
∠ADF=∠DEC,
AF=DC,,
∴△AFD≌△DCE(AAS),
∴△CDE的面积=△AFD的面积=![]()
∵矩形ABCD的面积=ABBC=2AB2,
∴2△ABE的面积=矩形ABCD的面积﹣2△CDE的面积=(2﹣![]() )AB2,
)AB2,
∴△ABE的面积=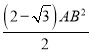 ,
,
∴ ,
,
故选:C.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目