题目内容
阅读理解:对于任意正实数a、b,∵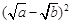 ≥0, ∴
≥0, ∴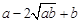 ≥0,
≥0,
∴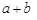 ≥
≥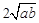 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在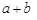 ≥
≥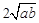 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥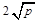 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值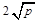 .
.
根据上述内容,回答下列问题:
若m>0,只有当m= 时,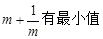 .
.
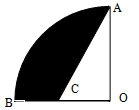
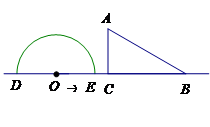
思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合),过点C作CD⊥AB,垂足为D,AD=a,DB=b.
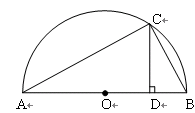
试根据图形验证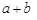 ≥
≥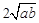 ,并指出等号成立时的条件.
,并指出等号成立时的条件.
探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线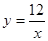 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.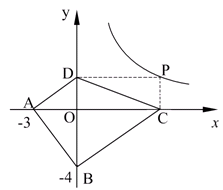
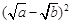 ≥0, ∴
≥0, ∴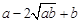 ≥0,
≥0,∴
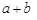 ≥
≥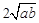 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.结论:在
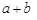 ≥
≥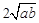 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥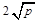 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值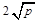 .
.根据上述内容,回答下列问题:
若m>0,只有当m= 时,
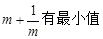 .
.思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合),过点C作CD⊥AB,垂足为D,AD=a,DB=b.

试根据图形验证
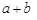 ≥
≥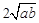 ,并指出等号成立时的条件.
,并指出等号成立时的条件. 探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线
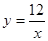 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
解:阅读理解:m= 1 (填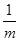 不扣分),最小值为 2 ;
不扣分),最小值为 2 ;
思考验证:∵AB是的直径,∴AC⊥BC,又∵CD⊥AB,∴∠CAD=∠BCD=90°-∠B,
∴Rt△CAD∽Rt△BCD, CD2=AD·DB, ∴CD=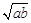
若点D与O不重合,连OC,在Rt△OCD中,∵OC>CD, ∴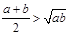 ,
,
若点D与O重合时,OC=CD,∴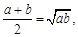
综上所述,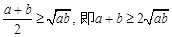 ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.
探索应用:设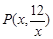 , 则
, 则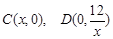 ,
,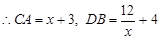 ,
,
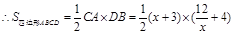 ,化简得:
,化简得: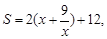
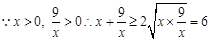 ,只有当
,只有当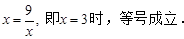
∴S≥2×6+12=24,
∴S四边形ABCD有最小值24.
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.
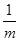 不扣分),最小值为 2 ;
不扣分),最小值为 2 ; 思考验证:∵AB是的直径,∴AC⊥BC,又∵CD⊥AB,∴∠CAD=∠BCD=90°-∠B,
∴Rt△CAD∽Rt△BCD, CD2=AD·DB, ∴CD=
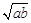
若点D与O不重合,连OC,在Rt△OCD中,∵OC>CD, ∴
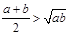 ,
, 若点D与O重合时,OC=CD,∴
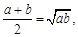
综上所述,
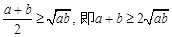 ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.探索应用:设
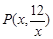 , 则
, 则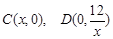 ,
,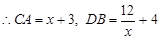 ,
,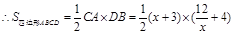 ,化简得:
,化简得: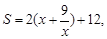
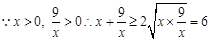 ,只有当
,只有当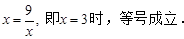
∴S≥2×6+12=24,
∴S四边形ABCD有最小值24.
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.
阅读理解:读懂题意即可得到结果;
思考验证:先证Rt△CAD∽Rt△BCD,根据相似三角形的对应边乘比例即可表示出CD,分两种情况讨论:
若点D与O不重合,连OC,在Rt△OCD中,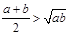 ;若点D与O重合,
;若点D与O重合,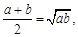
综上所述,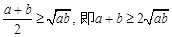 ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.
探索应用:设出点P的坐标,即可表示出CA、DB,从而得到四边形ABCD面积的函数关系式,根据函数关系式的特征即可得到结果。
思考验证:先证Rt△CAD∽Rt△BCD,根据相似三角形的对应边乘比例即可表示出CD,分两种情况讨论:
若点D与O不重合,连OC,在Rt△OCD中,
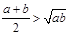 ;若点D与O重合,
;若点D与O重合,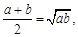
综上所述,
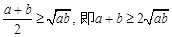 ,当CD等于半径时,等号成立.
,当CD等于半径时,等号成立.探索应用:设出点P的坐标,即可表示出CA、DB,从而得到四边形ABCD面积的函数关系式,根据函数关系式的特征即可得到结果。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
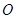 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦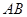 是小圆的切线.若大圆半径为
是小圆的切线.若大圆半径为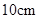 ,小圆半径为
,小圆半径为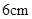 ,则弦
,则弦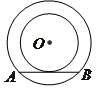
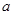 ,圆心在原点的圆(如图1),如果固定直径
,圆心在原点的圆(如图1),如果固定直径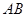 ,把圆内的所有与
,把圆内的所有与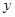 轴平行的弦都压缩到原来的
轴平行的弦都压缩到原来的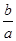 倍,就得到一种新的图形
倍,就得到一种新的图形 椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .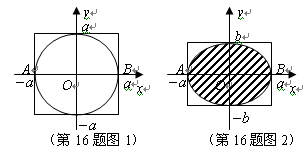
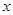 轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为
轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为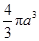 ,则此椭球的体积为 .
,则此椭球的体积为 .