题目内容
【题目】如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥CF于点G,连接AG.
(1)求证:∠ABG=∠ACF;
(2)用等式表示线段CG,AG,BG之间的等量关系,并证明.

【答案】(1)证明见解析;(2)CG=![]() AG+BG,证明见解析.
AG+BG,证明见解析.
【解析】
(1)根据等腰直角三角形的性质解答即可;
(2)在CG上截取CH=BG,连接AH,利用全等三角形的判定和性质解答即可.
(1)证明:
∵∠CAB=90°.
∵BG⊥CF于点G,
∴∠BGF=∠CAB=90°.
∵∠GFB=∠CFA
∴∠ABG=∠ACF
(2)CG=![]() AG+BG
AG+BG
在CG上截取CH=BG,连接AH,
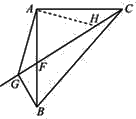
∵△ABC是等腰直角三角形,
∴∠CAB=90°,AB=AC.
∵∠ABG=∠ACH.
∴△ABG≌△ACH,
∴AG=AH,∠GAB=∠HAC.
∴∠GAH=90°.
∴AG2+AH2=GH2.
∴GH=![]() AG,
AG,
∴CG=CH+GH=![]() AG+BG,
AG+BG,

练习册系列答案
相关题目