题目内容
【题目】综合与实践
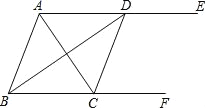
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
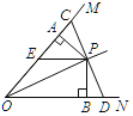
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)①直接得出结论;
②借助问题情景即可得出结论;
(2)先判断出∠BCE+∠BEC=90°,进而判断出∠BEC=∠BCG,得出△GHC≌△CBE,判断出AD=BC,进而判断出HC=BH,即可得出结论;
(3)先判断出四边形BENM为矩形,进而得出∠1+∠2=90°,再判断出∠1=∠3,得出△ENF≌△EBC,即可得出结论.
(1)①依据1:两条直线被一组平行线所截,所得的对应线段成比例(或平行线分线段成比例).
依据2:等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合(或等腰三角形的“三线合一”).
②答:点A在线段GF的垂直平分线上.
理由:由问题情景知,AM⊥DE,
∵四边形DEFG是正方形,
∴DE∥FG,
∴点A在线段GF的垂直平分线上.
(2)证明:过点G作GH⊥BC于点H,
∵四边形ABCD是矩形,点E在AB的延长线上,
∴∠CBE=∠ABC=∠GHC=90°,
∴∠BCE+∠BEC=90°.
∵四边形CEFG为正方形,
∴CG=CE,∠GCE=90°,
∴∠BCE+∠BCG=90°.
∴∠2BEC=∠BCG.
∴△GHC≌△CBE.
∴HC=BE,
∵四边形ABCD是矩形,
∴AD=BC.
∵AD=2AB,BE=AB,
∴BC=2BE=2HC,
∴HC=BH.
∴GH垂直平分BC.
∴点G在BC的垂直平分线上.
(3)答:点F在BC边的垂直平分线上(或点F在AD边的垂直平分线上).
过点F作FM⊥BC于点M,过点E作EN⊥FM于点N.
∴∠BMN=∠ENM=∠ENF=90°.
∵四边形ABCD是矩形,点E在AB的延长线上,
∴∠CBE=∠ABC=90°,
∴四边形BENM为矩形.
∴BM=EN,∠BEN=90°.
∴∠1+∠2=90°.
∵四边形CEFG为正方形,
∴EF=EC,∠CEF=90°.
∴∠2+∠3=90°.
∴∠1=∠3.
∵∠CBE=∠ENF=90°,
∴△ENF≌△EBC.
∴NE=BE.∴BM=BE.
∵四边形ABCD是矩形,
∴AD=BC.
∵AD=2AB,AB=BE.
∴BC=2BM.
∴BM=MC.
∴FM垂直平分BC.
∴点F在BC边的垂直平分线上.

 阅读快车系列答案
阅读快车系列答案