题目内容
【题目】如图,在平面直角坐标系中,0是坐标原点,点A坐标为(2, 0),点B坐标为(0, b) (b>0), 点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q.
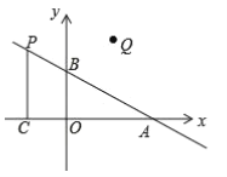
(1)当b=1时:①求直线AB相应的函数表达式:②若![]() ,求点P的坐标:
,求点P的坐标:
(2)设点P的横坐标为a,是否同时存在a、b,使得![]() 是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
【答案】(1)①![]() ;②P(
;②P(![]() );(2)存在,a=-2,b=2;或a=
);(2)存在,a=-2,b=2;或a=![]() ,b=1.
,b=1.
【解析】
(1)①由题意确定出B坐标,设直线AB解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可求出AB解析式;②由QO=QA以及OA的长,确定出Q横坐标,根据P与Q关于y轴对称,得出P横坐标,代入直线AB解析式求出纵坐标,即可确定出P坐标;
(2)同时存在a、b,使得△QAC是等腰直角三角形,分两种情况考虑:①若∠QAC=90°;②若∠AQC=90°,分别求出a与b的值即可.
解:(1)①当b=1时,B(0,1)
由A(2,0),B(0,1),
设直线AB解析式为![]() ,
,
把A与B坐标代入得:
![]() ,
,
解得: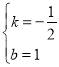
则直线AB解析式为![]()
②∵A(2,0),
∴ OA=2
∵QA=QO,OA=2,
∴Q点横坐标为xQ=1,
∵点P关于y轴的对称点为Q,
∴P点的横坐标为xP=-1,
代入直线AB解析式![]() ,
,
得![]() ,
,
则P坐标得P(![]() )
)
(2)①若∠QAC=90°,如图1所示,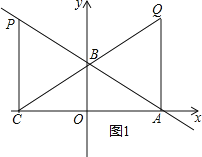
∴Q点的横坐标为xQ=2,
∴P点的横坐标为a=xP=-2,
∴AC=AQ=4,
∴Q(2,4)
即P(-2,4),
设直线AP的解析式为![]()
将P(-2,4),A(2,0)代入得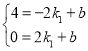
解得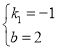
∴直线AP解析式为![]() ,
,
∴a=-2,b=2;
②如图2,若∠AQC=90°且QA=QC时,过点Q作QH⊥x轴于点H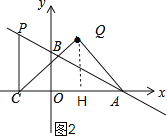
∴QH=CH=AH=![]() AC,
AC,
∴P点的横坐标为a,
∴Q点的横坐标为-a,
Q的横坐标![]() ,解得a=
,解得a=![]() ,-a=
,-a=![]()
Q的纵坐标QH=![]() AC=
AC=![]() =
=![]()
∴Q(![]() ,
,![]() ),P(
),P(![]() ,
,![]() )
)
设直线AP的解析式为![]()
将P(![]() ,
,![]() ),A(2,0)代入得
),A(2,0)代入得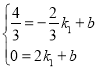
解得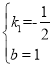
∴直线AP解析式为![]() ,
,
∴b=1,
∴a=![]() ,b=1,
,b=1,
综上所示,∴a=-2,b=2;或a=![]() ,b=1.
,b=1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】一手机经销商计划购进华为品牌![]() 型、
型、![]() 型、
型、![]() 型三款手机共
型三款手机共![]() 部,每款手机至少要购进
部,每款手机至少要购进![]() 部,且恰好用完购机款61000元.设购进
部,且恰好用完购机款61000元.设购进![]() 型手机
型手机![]() 部,
部,![]() 型手机
型手机![]() 部.三款手机的进价和预售价如下表:
部.三款手机的进价和预售价如下表:
手机型号 |
|
|
|
进价(单位:元/部) |
|
|
|
预售价(单位:元/部) |
|
|
|
(1)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润W(元)与x(部)之间的关系式;
(注;预估利润W=预售总额![]() 购机款
购机款![]() 各种费用)
各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
【题目】某铁路桥长1000米.现有一列火车从桥上匀速通过.测得火车从开始上桥到完全通过桥共用了1分钟(即从车头进入桥头到车尾离开桥尾),整个火车完全在桥上的时间为40秒.
(1)如果设这列火车的长度为x米,填写下表(不需要化简):
火车行驶过程 | 时间(秒) | 路程(米) | 速度(米/秒) |
完全通过桥 | 60 | ||
整列车在桥上 | 40 |
(2)求这列火车的长度.