题目内容
【题目】一手机经销商计划购进华为品牌![]() 型、
型、![]() 型、
型、![]() 型三款手机共
型三款手机共![]() 部,每款手机至少要购进
部,每款手机至少要购进![]() 部,且恰好用完购机款61000元.设购进
部,且恰好用完购机款61000元.设购进![]() 型手机
型手机![]() 部,
部,![]() 型手机
型手机![]() 部.三款手机的进价和预售价如下表:
部.三款手机的进价和预售价如下表:
手机型号 |
|
|
|
进价(单位:元/部) |
|
|
|
预售价(单位:元/部) |
|
|
|
(1)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润W(元)与x(部)之间的关系式;
(注;预估利润W=预售总额![]() 购机款
购机款![]() 各种费用)
各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
【答案】(1)![]()
![]() ;(2)①
;(2)①![]() ②预估利润的最大值是17500元,此时购进A型手机34部,B型手机18部,C型手机8部.
②预估利润的最大值是17500元,此时购进A型手机34部,B型手机18部,C型手机8部.
【解析】
(1)关键描述语:A型、B型、C型三款手机共60部,由A、B型手机的部数可表示出C型的手机的部数.根据购机款列出等式可表示出x、y之间的关系.根据题干,求出x的取值范围.
(2)①由预估利润W=预售总额﹣购机款﹣各种费用,列出等式即可.
②利用一次函数的增减性,结合(1)中求得的x的取值范围,即可确定最大利润和各种手机的购买数量.
解:(1)C手机的部数为![]() ;因为购进手机总共用了61000原,所以
;因为购进手机总共用了61000原,所以
![]()
整理得,![]()
根据题意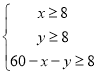 得:
得: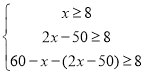
解得:![]()
故![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为:![]()
![]()
(2)①根据题意可知:
![]()
整理得,![]()
将(1)中![]() 代入以上关系式中,得
代入以上关系式中,得
![]()
整理得,
![]()
②根据![]() 可知:W是关于x的一次函数,且W随x的增大而增大
可知:W是关于x的一次函数,且W随x的增大而增大
∴当x=34时,W取最大值,![]()
将x=34分别代入![]() ,
,![]() 中,整理得:
中,整理得:
![]() ,
,![]()
即预估利润的最大值是17500元,此时购进A型手机34部,B型手机18部,C型手机8部.

【题目】长江中下游地区特大旱情发生后,全国人民抗旱救灾,众志成城.市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?