题目内容
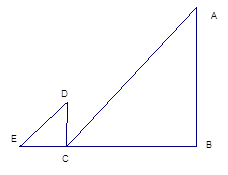
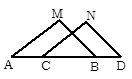
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是 ▲ ,△EDC与△ABC的面积之比为 ▲ 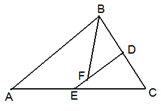

3,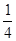
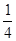
分析:首先根据条件D、E分别是BC、AC的中点可得DE∥AB,再求出∠BFD=∠DBF,根据等角对等边可得到DB=DF,再证明△ABC∽△EDC,可得到对应变成比例,根据相似三角形的面积比等于相似比的平方可得到答案.
解:∵△ABC中,D、E分别是BC、AC的中点,
∴DE∥AB,BD=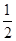 BC=3,
BC=3,
∴∠ABF=∠BFD,
∵BF平分∠ABC,
∴∠FBC=∠ABF,
∴∠BFD=∠DBF,
∴DB=DF=3,
∵DE∥AB,
∴△ABC∽△EDC,
∵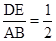 ,
,
∴△EDC与△ABC的面积之比为: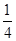
故答案为:3,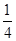
解:∵△ABC中,D、E分别是BC、AC的中点,
∴DE∥AB,BD=
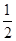 BC=3,
BC=3,∴∠ABF=∠BFD,
∵BF平分∠ABC,
∴∠FBC=∠ABF,
∴∠BFD=∠DBF,
∴DB=DF=3,
∵DE∥AB,
∴△ABC∽△EDC,
∵
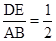 ,
,∴△EDC与△ABC的面积之比为:
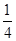
故答案为:3,

练习册系列答案
相关题目
 是
是 的中点;(
的中点;( ∽△
∽△ ;
; 。
。

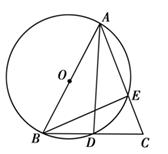
 内接于
内接于 ,
,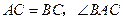 的平分线
的平分线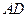 与
与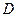 ,与
,与 交于点
交于点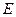 ,延长
,延长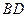 ,与
,与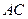 的延长线交于点
的延长线交于点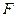 ,连接
,连接 是
是 的中点,连结
的中点,连结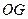 .
.
 ;
;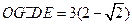 ,求
,求 ,则
,则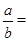 .
.