题目内容
【题目】已知二次函数y=x2-(2m-1)x+m2-m(m是常数)
(1)当m=2时,求二次函数图象与x轴的交点;
(2)若A(n-3,n2+2),B(-n+1,n2+2)是该二次函数图象上的两个不同点,求m的值和二次函数解析式.
【答案】(1)交点是(1,0)和(2,0);(2)m=![]() ,二次函数解析式为:y=x2+2x+
,二次函数解析式为:y=x2+2x+![]() .
.
【解析】
(1)将m=2代入函数解析式,然后令y=0,解一元二次方程即可得到图像与x轴的交点坐标;
(2)由A、B纵坐标相同,可知A、B关于对称轴对称,可求出对称轴,利用对称轴公式可求出m,从而得到二次函数解析式.
(1)当m=2时,y=x2-3x+2,
令y=0,得x2-3x+2=0,
解得:x1=1,x2=2,
∴交点是(1,0)和(2,0)
(2)∵A(n-3,n2+2)、B(-n+1,n2+2)是该二次函数图象上的两个不同点,
∴抛物线的对称轴是:![]() ,
,
∴ ![]() =,
=,![]() ,
,
将![]() 代入y=x2-(2m-1)x+m2-m,得
代入y=x2-(2m-1)x+m2-m,得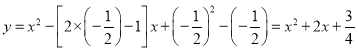 ,
,
∴二次函数解析式为:y=x2+2x+![]() .
.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目