ћвƒњƒЏ»Ё
°Њћвƒњ°њ…иЋЂ«ъѕяy£љ![]() £®k£Њ0£©”л÷±ѕяy£љxљї”ЏA\BЅљµг£®µгA‘ЏµЏ»эѕуѕё£©£ђљЂЋЂ«ъѕя‘ЏµЏ“їѕуѕёµƒ“ї÷І—Ў…дѕяBAµƒЈљѕт∆љ“∆£ђ є∆дЊ≠єэµгA£ђљЂЋЂ«ъѕя‘ЏµЏ»эѕуѕёµƒ“ї÷І—Ў…дѕяABµƒЈљѕт∆љ“∆£ђ є∆дЊ≠єэµгB£ђ∆љ“∆ЇуµƒЅљћх«ъѕяѕаљї”ЏP°ҐQЅљµг£ђіЋ ±ќ“√«≥∆∆љ“∆ЇуµƒЅљћх«ъѕяЋщќІ≤њЈ÷£®»зЌЉ÷–“х”∞≤њЈ÷£©ќ™ЋЂ«ъѕяµƒ°∞нш°±£ђPQќ™ЋЂ«ъѕяµƒ°∞ншЊґ°∞£ђµ±ЋЂ«ъѕяy£љ
£®k£Њ0£©”л÷±ѕяy£љxљї”ЏA\BЅљµг£®µгA‘ЏµЏ»эѕуѕё£©£ђљЂЋЂ«ъѕя‘ЏµЏ“їѕуѕёµƒ“ї÷І—Ў…дѕяBAµƒЈљѕт∆љ“∆£ђ є∆дЊ≠єэµгA£ђљЂЋЂ«ъѕя‘ЏµЏ»эѕуѕёµƒ“ї÷І—Ў…дѕяABµƒЈљѕт∆љ“∆£ђ є∆дЊ≠єэµгB£ђ∆љ“∆ЇуµƒЅљћх«ъѕяѕаљї”ЏP°ҐQЅљµг£ђіЋ ±ќ“√«≥∆∆љ“∆ЇуµƒЅљћх«ъѕяЋщќІ≤њЈ÷£®»зЌЉ÷–“х”∞≤њЈ÷£©ќ™ЋЂ«ъѕяµƒ°∞нш°±£ђPQќ™ЋЂ«ъѕяµƒ°∞ншЊґ°∞£ђµ±ЋЂ«ъѕяy£љ![]() £®k£Њ0£©µƒншЊґќ™6 ±£ђkµƒ÷µќ™£®°°°°£©
£®k£Њ0£©µƒншЊґќ™6 ±£ђkµƒ÷µќ™£®°°°°£©
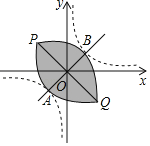
A.![]() B.2C.
B.2C.![]() D.3
D.3
°Њір∞Є°њA
°Њљвќц°њ
“‘PQќ™±я£ђ„чЊЎ–ќPQQ°дP°дљїЋЂ«ъѕя”ЏµгP°д°ҐQ°д£ђЅ™ЅҐ÷±ѕяABЉ∞ЋЂ«ъѕяљвќц љ≥…Јљ≥ћ„й£ђЌ®єэљвЈљ≥ћ„йњ…«у≥цµгA°ҐBµƒ„ш±к£ђ”…PQµƒ≥§ґ»њ…µ√≥цµгPµƒ„ш±к£®µгP‘Џ÷±ѕяy£љx…ѕ£©£ђ”…ЌЉ–ќµƒґ‘≥∆–‘љбЇѕµгA°ҐBЇЌPµƒ„ш±књ…µ√≥цµгP°дµƒ„ш±к£ђ‘ўјы”√Јі±»јэЇѓ эЌЉѕу…ѕµгµƒ„ш±кћЎ’чЉіњ…µ√≥цєЎ”Џkµƒ“ї‘™“їіќЈљ≥ћ£ђљв÷ЃЉіњ…µ√≥цљб¬џ£Ѓ
“‘PQќ™±я£ђ„чЊЎ–ќPQQ°дP°дљїЋЂ«ъѕя”ЏµгP°д°ҐQ°д£ђ»зЌЉЋщ Њ£Ѓ
Ѕ™ЅҐ÷±ѕяABЉ∞ЋЂ«ъѕяљвќц љ≥…Јљ≥ћ„й£ђ![]() £ђ
£ђ
љвµ√£Ї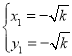 £ђ
£ђ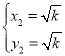 £ђ
£ђ
°аµгAµƒ„ш±кќ™£®©Б![]() £ђ©Б
£ђ©Б![]() £©£ђµгBµƒ„ш±кќ™£®
£©£ђµгBµƒ„ш±кќ™£®![]() £ђ
£ђ![]() £©£Ѓ
£©£Ѓ
°яPQ£љ6£ђ
°аOP£љ3£ђµгPµƒ„ш±кќ™£®©Б![]() £ђ
£ђ![]() £©£Ѓ
£©£Ѓ
ЄщЊЁЌЉ–ќµƒґ‘≥∆–‘њ…÷™£ЇPP°д£љAB£љQQ°д£ђ
°аµгP°дµƒ„ш±кќ™£®©Б![]() +2
+2![]() £ђ
£ђ![]() +2
+2![]() £©£Ѓ
£©£Ѓ
”÷°яµгP°д‘ЏЋЂ«ъѕяy£љ![]() …ѕ£ђ
…ѕ£ђ
°а£®©Б![]() +2
+2![]() £©£®
£©£®![]() +2
+2![]() £©£љk£ђ
£©£љk£ђ
љвµ√£Їk£љ![]() £Ѓ
£Ѓ
є —°£ЇA£Ѓ


°Њћвƒњ°њƒ≥…ћ≥°Њ≠”™ƒ≥÷÷∆Ј≈∆µƒЌжЊя£ђєЇљш ±µƒµ•Љџ «20‘™£ђЄщЊЁ –≥°µч≤й£Ї‘Џ“їґќ ±ЉдƒЏ£ђѕъ џµ•Љџ «30‘™ ±£ђѕъ џЅњ «500Љю£ђґшѕъ џµ•Љџ√њ…ѕ’«1‘™£ђЊЌїб…ў џ≥ц10ЉюЌжЊя£Ѓ
£®1£©≤їЈЅ…иЄ√÷÷∆Ј≈∆ЌжЊяµƒѕъ џµ•Љџќ™x‘™£®x£Њ30£©£ђ«лƒгЈ÷±р”√xµƒіъ э љјі±н Њѕъ џЅњyЉюЇЌѕъ џЄ√∆Ј≈∆ЌжЊяїсµ√јы»уw‘™£ђ≤Ґ∞—љбєыћо–і‘Џ±нЄс÷–£Ї
ѕъ џµ•Љџ£®‘™£© | x£®x£Њ30£© |
ѕъ џЅњy£®Љю£© | °° °° |
ѕъ џЌжЊяїсµ√јы»уw£®‘™£© | °° °° |
£®2£©‘ЏµЏ£®1£©ќ µƒћхЉюѕ¬£ђ»ф…ћ≥°їсµ√ЅЋ8750‘™ѕъ џјы»у£ђ«уЄ√ЌжЊяѕъ џµ•Љџx”¶ґ®ќ™ґа…ў‘™£њ
£®3£©‘ЏµЏ£®1£©ќ µƒћхЉюѕ¬£ђ»фЌжЊя≥Ієжґ®Є√∆Ј≈∆ЌжЊяѕъ џµ•Љџ≤їµЌ”Џ32‘™£ђ«“…ћ≥°“™Ќк≥…≤ї…ў”Џ400Љюµƒѕъ џ»ќќс£ђ«у£Ї…ћ≥°ѕъ џЄ√∆Ј≈∆ЌжЊяїсµ√„оіујы»у «ґа…ў£њ