题目内容
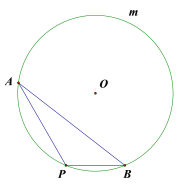
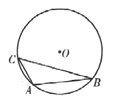
【题目】如图，△ABC内接于⊙O，BC=6，AC=2，∠A-∠B=90°，则⊙O的面积为( )
A.9.6πB.10πC.10.8πD.12π
【答案】B
【解析】
过点B作圆的直径BE交圆于点E，由直径所对的圆周角是直角可得∠ECB=90°，再根据圆内接四边形的对角互补，推出
，然后由勾股定理求出圆的直径，即可求出圆面积.
如下图所示，过点B作圆的直径BE交圆于点E,
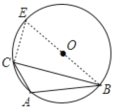
则∠ECB=90°，
∴∠E+∠EBC=90°，
∵圆的内接四边形对角互补,
∴∠E+∠A=180°①，
∵∠A∠ABC=90°②，
①-②可得：∠E+∠ABC=90°，
∴∠ABC=∠EBC，
∴，
∴CE=AC=2，
在Rt△BCE中，由勾股定理得，
，
∴⊙O的半径为
，
∴圆的面积=
，
故选B.
练习册系列答案
相关题目
