题目内容
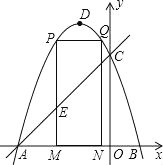
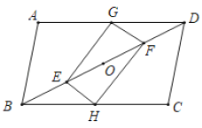
【题目】如图,在矩形BCOG中,OC=3,点A为边OG上一点,OA=![]() ,AB,∠CBA=30°.动点D以每秒1个单位的速度从点C出发沿CO向终点O运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动,过点D作DF∥AB,交BC于点F,连接AD、DE、EF,设运动时间为1秒.
,AB,∠CBA=30°.动点D以每秒1个单位的速度从点C出发沿CO向终点O运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动,过点D作DF∥AB,交BC于点F,连接AD、DE、EF,设运动时间为1秒.
(1)求DF的长(用含t的代数式表示)
(2)求证:四边形ADFE为平行四边形;
(3)探索当t为何值时,△BEF与以D,E,F为顶点的三角形相似?
【答案】(1)DF=2t;(2)见解析;(3) t=![]() 或t=
或t=![]()
【解析】
(1)在直角三角形中,30°对应的直角边为斜边的一半;
(2)对边相等且平行的四边形ADFE为平行四边形;
(3)分2种情况讨论。
(1)∵DF∥AB,
∴∠CFD=∠CBA=30°,
∵△CDF是直角三角形,∠CFD=30°
∴DF=2CD=2t;
(2)∵动点E以每秒2个单位的速度从点A出发沿AB向点B运动,
∴AE=2t,
∴DF=AE=2t,
∵DF∥AB,
∴四边形ADEF是平行四边形;
(3)在直角三角形AGB中,∠AGB=90°,
∠GAB=∠CBA=30°,BG=OC=3
∴AB=2BG=6,
∵DF∥AB,
∴∠BEF=∠DFE.
分两种情况:
①当∠BFE=∠DEF时,则△BEF∽△DFE,此时DE∥BC,即四边形DEBF是平行四边形,
∴DF=BE,而DF=2t,BE=6﹣2t,
∴2t=6﹣2t,
解得t=![]() ;
;
②当∠BFE=∠FDE时,则△BEF∽△EFD,
∴![]() ,
,
即EF2=DF×BE,
∵四边形ADEF是平行四边形,即EF=AD,
又AD2=OD2+OA2,
∴(3﹣t)2+(![]() )2=2t×(6﹣2t),
)2=2t×(6﹣2t),
解得t=![]()
综上所述,t=![]() 或t=
或t=![]()

练习册系列答案
相关题目