题目内容
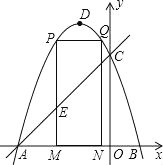
【题目】如图,在平面直角坐标系中,抛物线y=x2+(1-m)x-m交x轴于A,B两点(点A在点B的左边),交y轴负半轴于点C.
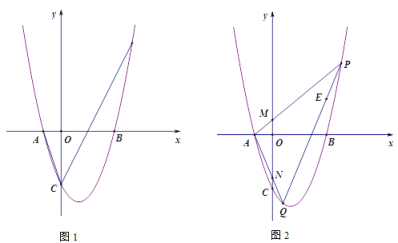
(1)如图1,m=3
①直接写出A,B,C三点的坐标;
②若抛物线上有一点D,∠ACD=45°,求点D的坐标;
(2)如图2,过点E(m,2)作一直线交抛物线于点P,Q两点,连接AP,AQ,分别交y轴于M,N两点,求证:OMON是一个定值.
【答案】(1)①A(-1,0),B(3,0),C(0,-3);②D(4,5);(2)见解析.
【解析】
(1)①将m=3代入抛物线y=x2+(1-m)x-m,得y=x2-2x-3,分别令x=0,y=0,即可得出A、B、C三点的坐标;
②过A作AK⊥AC交CD于点K,作KH⊥x轴于点H,证明△OAC≌△HKA,可得K(2,1),用待定系数法求出直线CD的解析式,与抛物线联立解即可得出D的坐标;
(2)由题意,可得A(-1,0),B(m,0),设P(x1,y1),Q(x2,y2),因为直线PQ过点E(m,2),可得其解析式为y=ax+2-am,与抛物线联立并消去y,得:x2+(1-m-a)x+am-m+2=0,所以x1+x2=a+m-1,x1x2=am-m-2,作PS⊥x轴于点S,作QT⊥x轴于点T,证明△AMO∽△APS,可得OM=x1-m,同理ON=-(x2-m),代入计算OMON,即可得出OMON是一个定值.
解:(1)①当m=3时,y=x2+(1-3)x-3 =x2-2x-3,
当x=0时,y=-3,
当y=0时,x2-2x-3=0,
解得:x=-1或x=3,
∴A(-1,0),B(3,0),C(0,-3);
②如图1,过A作AK⊥AC交CD于点K,作KH⊥x轴于点H,

∵∠ACD=45°,
∴AC=AK,
∵∠AOC=∠KHA=90°,∠ACO=90°-∠OAC=∠KAH,
∴△OAC≌△HKA(AAS),
∴AH=CO=3,KH=OA=1,
∴K(2,1),
设直线CD的解析式为y=kx-3
∴2k-3=1,
∴k=2,
∴设直线CD的解析式为y=2x-3,
联立![]() ,
,
解得x=0(舍去),或x=4,
∴D(4,5);
(2)∵y=x2+(1-m)x-m,

当y=0时,x2+(1-m)x-m=0,
解得x=-1或x=m,
∴A(-1,0),B(m,0),
∵过点E(m,2)作一直线交抛物线于P、Q两点,
设直线PQ的解析式为y=ax+b,P(x1,y1),Q(x2,y2),
∴2=am+b,b=2-am,
∴直线PQ的解析式为y=ax+2-am,
联立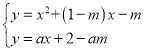 ,
,
消去 y,得:x2+(1-m-a)x+am-m-2=0,
∴x1+x2=a+m-1,x1x2=am-m-2,
如图2,作PS⊥x轴于点S,作QT⊥x轴于点T,
∴PS∥y轴,
∴△AMO∽△APS,
∴![]() ,即
,即![]() ,
,
∴OM=x1-m,
同理,ON=-(x2-m),
∴OMON=-(x1-m)(x2-m)=[x1x2m(x1+x2)+m2]=-[am-m-2-m(a+m-1)+m2]=2,为定值.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案【题目】某商场经营某种品牌的玩具,购进时的单价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每上涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x(x>30) |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在第(1)问的条件下,若商场获得了8750元销售利润,求该玩具销售单价x应定为多少元?
(3)在第(1)问的条件下,若玩具厂规定该品牌玩具销售单价不低于32元,且商场要完成不少于400件的销售任务,求:商场销售该品牌玩具获得最大利润是多少?