ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§Βψ![]() «’ΐΖΫ–Έ
«’ΐΖΫ–Έ![]() ±Ώ
±Ώ![]() …œ»Έ“β“ΜΒψΘ§“‘
…œ»Έ“β“ΜΒψΘ§“‘![]() ΈΣ±ΏΉς’ΐΖΫ–Έ
ΈΣ±ΏΉς’ΐΖΫ–Έ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§Βψ
Θ§Βψ![]() «œΏΕΈ
«œΏΕΈ![]() ÷–ΒψΘ§…δœΏ
÷–ΒψΘ§…δœΏ![]() ”κ
”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°
Θ°
Θ®1Θ©«κ÷±Ϋ”–¥≥ω![]() ΚΆ
ΚΆ![]() ΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΘ°
ΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΘ°
Θ®2Θ©Α―ΆΦ1÷–ΒΡ’ΐΖΫ–Έ![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() Θ§¥Υ ±Βψ
Θ§¥Υ ±Βψ![]() «ΓΚΟ¬δ‘ΎœΏΕΈ
«ΓΚΟ¬δ‘ΎœΏΕΈ![]() …œΘ§»γΆΦ2Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§Θ®1Θ©÷–ΒΡΫα¬έ «Ζώ≥…ΝΔΘ§«κΥΒΟςάμ”…Θ°
…œΘ§»γΆΦ2Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§Θ®1Θ©÷–ΒΡΫα¬έ «Ζώ≥…ΝΔΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©Α―ΆΦ1÷–ΒΡ’ΐΖΫ–Έ![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() Θ§¥Υ ±Βψ
Θ§¥Υ ±Βψ![]() ΓΔ
ΓΔ![]() «ΓΚΟΖ÷±π¬δ‘ΎœΏΕΈ
«ΓΚΟΖ÷±π¬δ‘ΎœΏΕΈ![]() ΓΔ
ΓΔ![]() …œΘ§Ν§Ϋ”
…œΘ§Ν§Ϋ”![]() Θ§»γΆΦ3Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§»τ
Θ§»γΆΦ3Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§»τ![]() Θ§
Θ§![]() Θ§÷±Ϋ”–¥≥ω
Θ§÷±Ϋ”–¥≥ω![]() ΒΡ≥ΛΕ»Θ°
ΒΡ≥ΛΕ»Θ°
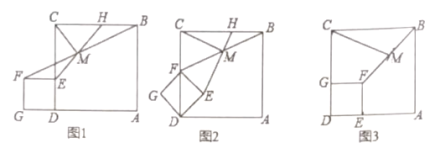
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©
ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©![]() .
.
ΓΨΫβΈωΓΩ
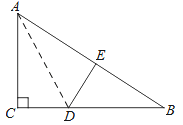
(1)÷ΛΟςΠΛFMEΓ’ΠΛAMHΘ§ΒΟΒΫHM=EMΘ§ΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟΫα¬έ. Θ®2Θ©ΗυΨί’ΐΖΫ–ΈΒΡ–‘÷ ΒΟΒΫΒψAΓΔEΓΔC‘ΎΆ§“ΜΧθ÷±œΏ…œ,άϊ”Ο÷±Ϋ«»ΐΫ«–Έ–±±Ώ…œΒΡ÷–œΏΒ»”Ύ–±±ΏΒΡ“ΜΑκΩ…÷Σ. Θ®3Θ©»γΆΦ3÷–Θ§Ν§Ϋ”ECΘ§EMΘ§”…Θ®1Θ©Θ®2Θ©Ω…÷ΣΘ§ΓςCME «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§άϊ”ΟΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΫβΨωΈ ΧβΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©Ϋα¬έΘΚCMΘΫMEΘ§CMΓΆEMΘ°
άμ”…ΘΚΓΏADΓΈEFΘ§ADΓΈBCΘ§
ΓύBCΓΈEFΘ§
ΓύΓœEFMΘΫΓœHBMΘ§
‘ΎΓςFMEΚΆΓςBMH÷–Θ§
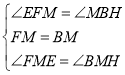
ΓύΓςFMEΓ’ΓςBMHΘ®ASAΘ©Θ§
ΓύHMΘΫEMΘ§EFΘΫBHΘ§
ΓΏCDΘΫBCΘ§
ΓύCEΘΫCHΘ§ΓΏΓœHCEΘΫ90ΓψΘ§HMΘΫEMΘ§
ΓύCMΘΫMEΘ§CMΓΆEMΘ°
Θ®2Θ©»γΆΦ2Θ§Ν§Ϋ”![]() Θ§
Θ§
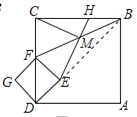
ΓΏΥΡ±Ώ–Έ![]() ΚΆΥΡ±Ώ–Έ
ΚΆΥΡ±Ώ–Έ![]() «’ΐΖΫ–ΈΘ§
«’ΐΖΫ–ΈΘ§
Γύ![]()
ΓύΒψ![]() ‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§
‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§
ΓΏ![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§
Γύ![]() Θ§
Θ§![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
ΓΏ![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]()
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
Θ®3Θ©»γΆΦ3÷–Θ§Ν§Ϋ”ECΘ§EMΘ°
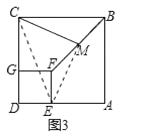
”…Θ®1Θ©Θ®2Θ©Ω…÷ΣΘ§ΓςCME «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓΏ![]()
ΓύCMΘΫEMΘΫ![]()

 »ΪΡή≤βΩΊΤΎΡ©–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
»ΪΡή≤βΩΊΤΎΡ©–ΓΉ¥‘ΣœΒΝ–¥πΑΗ