题目内容
在直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C =60°，AD=DC=2
，则BC= 。
，则BC= 。3
根据题意作图过点D作DE⊥BC于点E，可把直角梯形分为矩形ABED和直角三角形DEC，分别根据矩形的性质和直角三角形的特性求得BE，EC的长，求和即可．
解：过点D作DE⊥BC于点E
∵AD∥BC，∠ABC=90°
∴∠A=90°
∵DE⊥BC
∴∠DEB=90°
∴四边形ABED是矩形，BE=AD=2
∵∠C=60°，DC=2
∴EC=
DC=
∴BC=BE+EC=2+=3．
解：过点D作DE⊥BC于点E
∵AD∥BC，∠ABC=90°
∴∠A=90°
∵DE⊥BC
∴∠DEB=90°
∴四边形ABED是矩形，BE=AD=2
∵∠C=60°，DC=2
∴EC=
DC=∴BC=BE+EC=2
+=3．
练习册系列答案
阅读快车系列答案
相关题目
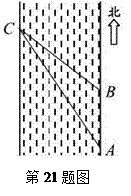
测得C在A北偏西31°的方向上，沿河岸向北前行40米到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，求这条河的宽度．（参考数值：tan31°≈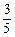
）
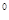,∠B=45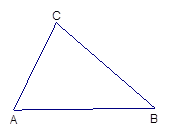
。
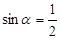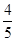
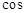В是关于x的方程kx2－kx+1=0的两个根,求∠B的度数. (11分)