题目内容
如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30º角,且此时测得1米杆的影长为2米,求电线杆的高度 

(14+2 )米
)米
 )米
)米分析:构造相应的直角三角形,利用勾股定理及影长与实物比求解.

解:如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.
∵∠DCE=30°,CD=8米,
∴CE=CD?cos∠DCE=8×
 =4
=4 (米),
(米),∴DE=4米,
设AB=x,EF=y,
∵DE⊥BF,AB⊥BF,
∴△DEF∽△ABF,
∴
 =
= ,即
,即 =
= …①,
…①,∵1米杆的影长为2米,根据同一时间物高与影长成正比可得,
 =
= …②,
…②,①②联立,解得x=14+2
 (米).
(米).故答案为:14+2
 .
.
练习册系列答案
相关题目
 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 垂直,
垂直, 厘米,
厘米, ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: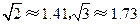 )
)

 ,则BC= 。
,则BC= 。 │+(
│+( -
- )=0,则∠C=_______
)=0,则∠C=_______
 °≈
°≈ ,
,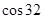 °≈
°≈ ,
, °≈
°≈ )
)