Question

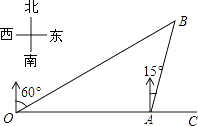
【题目】如图1，已知点A（2，0），B（0，4），∠AOB的平分线交AB于C，一动点P从O点出发，以每秒2个单位长度的速度，沿y轴向点B作匀速运动，过点P且平行于AB的直线交x轴于Q，作P、Q关于直线OC的对称点M、N．设P运动的时间为t（0＜t＜2）秒．

（1）求C点的坐标，并直接写出点M、N的坐标（用含t的代数式表示）；
（2）设△MNC与△OAB重叠部分的面积为S．
①试求S关于t的函数关系式；
②在图2的直角坐标系中，画出S关于t的函数图象，并回答：S是否有最大值？若有，写出S的最大值；若没有，请说明理由．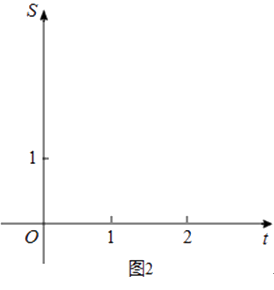

Answer 1

【答案】
（1）

解：如答图1，过点C作CF⊥x轴于点F，CE⊥y轴于点E，

由题意，易知四边形OECF为正方形，设正方形边长为x．

∵CE∥x轴，

∴ ，即 ，解得x= ．

∴C点坐标为（ ， ）；

∵PQ∥AB，

∴ ，即 ，

∴OP=2OQ．

∵P（0，2t），

∴Q（t，0）．

∵对称轴OC为第一象限的角平分线，

∴对称点坐标为：M（2t，0），N（0，t）．

（2）

解：①当0＜t≤1时，如答图2﹣1所示，点M在线段OA上，重叠部分面积为S△CMN．

S△CMN=S四边形CMON﹣S△OMN

=（S△COM+S△CON）﹣S△OMN

=（ 2t× + t× ）﹣ 2tt

=﹣t2+2t；

当1＜t＜2时，如答图2﹣2所示，点M在OA的延长线上，设MN与AB交于点D，则重叠部分面积为S△CDN．

设直线MN的解析式为y=kx+b，将M（2t，0）、N（0，t）代入得 ，

解得 ，

∴y=﹣ x+t；

同理求得直线AB的解析式为：y=﹣2x+4．

联立y=﹣ x+t与y=﹣2x+4，求得点D的横坐标为 ．

S△CDN=S△BDN﹣S△BCN

= （4﹣t） ﹣ （4﹣t）×

= t2﹣2t+ ．

综上所述，S= ．

②画出函数图象，如答图2﹣3所示：

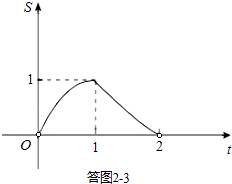
观察图象，可知当t=1时，S有最大值，最大值为1．

【解析】（1）如答图1，作辅助线，由比例式求出点D的坐标；（2）①所求函数关系式为分段函数，需要分类讨论．答图2﹣1，答图2﹣2表示出运动过程中重叠部分（阴影）的变化，分别求解；②画出函数图象，由两段抛物线构成．观察图象，可知当t=1时，S有最大值．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．