��Ŀ����
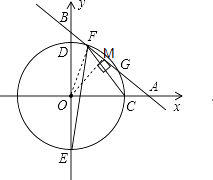
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У�һ�κ���y=�� ![]() x+b��bΪ������b��0����ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B���뾶Ϊ4�ġ�O��x���������ཻ�ڵ�C����y���ཻ�ڵ�D��E����D�ڵ�E�Ϸ���
x+b��bΪ������b��0����ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B���뾶Ϊ4�ġ�O��x���������ཻ�ڵ�C����y���ཻ�ڵ�D��E����D�ڵ�E�Ϸ��� 
��1����ֱ��AB�� ![]() ����������F��G�� �����CFE�Ķ�����
����������F��G�� �����CFE�Ķ�����
���ú�b�Ĵ���ʽ��ʾFG2 �� ��ֱ��д��b��ȡֵ��Χ��
��2����b��5�����߶�AB���Ƿ���ڵ�P��ʹ��CPE=45�㣿�����ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺����ͼ��

�ߡ�COE=90��
���CFE= ![]() ��COE=45�㣬��Բ�ܽǶ�����
��COE=45�㣬��Բ�ܽǶ�����
�ڷ���һ��
��ͼ����OM��AB��M������OF��
��OM��AB��ֱ�ߵĺ���ʽΪ��y=�� ![]() x+b��
x+b��
��OM���ڵ�ֱ�ߺ���ʽΪ��y= ![]() x��
x��
�ཻ��M�� ![]() b��
b�� ![]() b��
b��
��OM2=�� ![]() b��2+��
b��2+�� ![]() b��2��
b��2��
��OF=4��
��FM2=OF2��OM2=42���� ![]() b��2����
b��2���� ![]() b��2��
b��2��
��FM= ![]() FG��
FG��
��FG2=4FM2=4��[42���� ![]() b��2����
b��2���� ![]() b��2]=64��
b��2]=64�� ![]() b2=64����1��
b2=64����1�� ![]() b2����
b2����
��ֱ��AB�� ![]() ����������F��G��
����������F��G��
��4��b��5��
��FG2=64����1�� ![]() b2�� ��4��b��5��
b2�� ��4��b��5��
��������
�� ��ͼ����OM��AB��M������OF��

��ֱ�ߵĺ���ʽΪ��y=�� ![]() x+b��
x+b��
��B��������0��b����A�������� ![]() b��0����
b��0����
��AB= ![]() =
= ![]() b��
b��
��sin��BAO= ![]() =
= ![]() =
= ![]() ��
��
��sin��MAO= ![]() =
= ![]() =
= ![]() ��
��
��OM= ![]() b��
b��
����RT��OMF��
FM= ![]() =
= ![]()
��FG=2FM��
��FG2=4FM2=4��42�� ![]() b2��=64����
b2��=64���� ![]() b2=64����1��
b2=64����1�� ![]() b2����
b2����
��ֱ��AB�� ![]() ����������F��G��
����������F��G��
��4��b��5��
��FG2=64����1�� ![]() b2�� ��4��b��5��
b2�� ��4��b��5��
��2���⣺��ͼ��

��b=5ʱ��ֱ����Բ���У�
����ֱ������ϵ�У���COE=90�㣬
���CPE=��ODC=45�㣬
����ڵ�P��ʹ��CPE=45�㣬
����OP��
��P���е㣬
��OP��AB��
���APO�ס�AOB��
�� ![]() =
= ![]() ��
��
��OP=r=4��OB=5��AO= ![]() ��
��
�� ![]() =
= ![]() ��AP=
��AP= ![]() ��
��
��AB= ![]() =
= ![]() =
= ![]() ��
��
��PM��AO��AO�ڵ�M����P������Ϊ��x��y����
�ߡ�AMP�ס�AOB��
�� ![]()
�� ![]() =
= ![]() ��
��
��y= ![]() ��
��
��x=OM= ![]() =
= ![]() =
= ![]()
���P�������� ![]() ��
�� ![]() ����
����
��b��5ʱ��ֱ����Բ���룬������P
����������1������CD��EA������ͬһ�������Ե�Բ�ܽ�������С�CFE=45�㣬��2����OM��AB��M������OF����������ֱ�ߴ�ֱ�ཻ�������M�����꣬���ù��ɶ������FM2 �� �����FG2 �� �ٸ���ʽ��д��b�ķ�Χ����3����b=5ʱ��ֱ����Բ���У����ڵ�P��ʹ��CPE=45�㣬�����á�APO�ס�AOB�͡�AMP�ס�AOB���Ƶó���P�����꣬�����OP���ڵ�ֱ�߽���ʽ��

����Ŀ��Ϊ���˽⡰ͨ��ʱ��������ͨ��ʱ����ָÿ��ͨ��ʱ�䣩�ķֲ������Сǿ�ռ�������1000����ͨ��ʱ�������ݣ���Щ���ݾ�������18�����ӣ��������������ȡ�����ɸ�������Ϊ������ͳ�ƽ�����±����������˲�������Ƶ���ֲ�ֱ��ͼ�� 
��ͨ��ʱ���� | 0��x��3 | 3��x��6 | 6��x��9 | 9��x��12 | 12��x��15 | 15��x��18 |
���� | 36 | a | 8 | 12 | 8 | 12 |
���ݱ���ͼ�ṩ����Ϣ�������������⣺
��1��a= �� ������������
��2���������С�ͨ��ʱ����������9���ӵ�Ƶ�ʣ���
��3�������Сǿ����1000��ͨ���С�ͨ��ʱ��������15���ӵĴ�����
����Ŀ���ס���������5�δ�в��������еĻ������£� �ף�8��8��7��8��9
�ң�5��9��7��10��9
��1��������
ƽ���� | ���� | ��λ�� | ���� | |
�� | 8 | 8 | 0.4 | |
�� | 9 | 3.2 |
��2������������5�γɼ���ѡ��ײμ����������������������ʲô��
��3������������1�Σ�����8������ô�ҵ�����ɼ��ķ��� �� ����������С�����䡱����
����Ŀ��ijУΪ�˽�2013����꼶ѧ�������鼮������������������ȡ��40��ѧ�������鼮�����������ͳ�ƽ���г����µı������Ƴ���ͼ��ʾ������ͳ��ͼ�����п��������ռ��40��ѧ�������ܲ�����40%�� 
��� | ������ | �̸��� | ������ | ���� |
���������� | 128 | 80 | m | 48 |
��1�����������ĸm��ֵ������ͳ��ͼ�С��̸��ࡱ����Ӧ��Բ�ĽǦ��Ķ�����
��2����У2013����꼶��500��ѧ����������Ƹ��꼶ѧ�������Ľ̸����鼮Լ���ٱ���