��Ŀ����
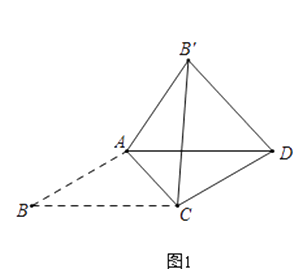
����Ŀ����ͼ������ABCD�ı�AB=3cm��AD=4cm����E�ӵ�A������������AD�ƶ�����CEΪֱ����ԲO����FΪԲO������BD�Ĺ����㣬����EF��CF������E��EG��EF��EG��ԲO�ཻ�ڵ�G������CG�� 
��1����˵���ı���EFCG�Ǿ��Σ�
��2����ԲO������BD����ʱ����Eֹͣ�ƶ����ڵ�E�ƶ��Ĺ����У� �پ���EFCG������Ƿ�������ֵ����Сֵ�������ڣ����������ֵ����Сֵ���������ڣ�˵�����ɣ�
�����G�ƶ�·�ߵij���
���𰸡�
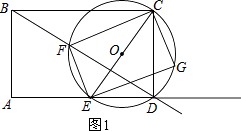
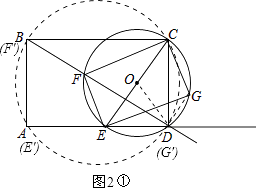
��1��֤������ͼ1��
��CEΪ��O��ֱ����
���CFE=��CGE=90�㣮
��EG��EF��
���FEG=90�㣮
���CFE=��CGE=��FEG=90�㣮
���ı���EFCG�Ǿ��Σ�
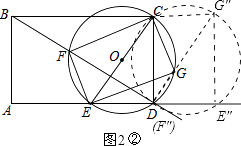
��2���⣺�ٴ��ڣ�
����OD����ͼ2�٣�
���ı���ABCD�Ǿ��Σ�
���A=��ADC=90�㣮
�ߵ�O��CE���е㣬
��OD=OC��
���D�ڡ�O�ϣ�
�ߡ�FCE=��FDE����A=��CFE=90�㣬
���CFE�ס�DAB��
�� ![]() =��
=�� ![]() ��2��
��2��
��AD=4��AB=3��
��BD=5��
S��CFE=�� ![]() ��2S��DAB
��2S��DAB
= ![]() ��
�� ![]() ��3��4
��3��4
= ![]() ��
��
��S����EFCG=2S��CFE
= ![]() ��
��
���ı���EFCG�Ǿ��Σ�
��FC��EG��
���FCE=��CEG��
�ߡ�GDC=��CEG����FCE=��FDE��
���GDC=��FDE��
�ߡ�FDE+��CDB=90�㣬
���GDC+��CDB=90�㣮
���GDB=90��
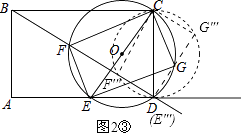
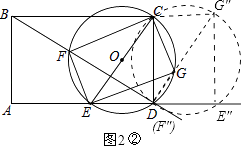
����E�ڵ�A��E�䣩��ʱ����F�ڵ�B��F�䣩������G�ڵ�D��G�䣩������ͼ2����ʾ��
��ʱ��CF=CB=4��
����F�ڵ�D��F�壩��ʱ��ֱ��F��G���BD��
��ͼ2����ʾ��
��ʱ��O������BD���У�CF=CD=3��
��CF��BDʱ��CF��С��
��ͼ2����ʾ��
S��BCD= ![]() BCCD=
BCCD= ![]() BDCF
BDCF
��4��3=5��CF
��CF= ![]() ��
��
�� ![]() ��CF��4��
��CF��4��
��S����EFCG= ![]() ��
��
�� ![]() ����
���� ![]() ��2��S����EFCG��
��2��S����EFCG�� ![]() ��42��
��42��
�� ![]() ��S����EFCG��12��
��S����EFCG��12��
�����EFCG��������ֵΪ12����СֵΪ ![]() ��
��
�ڡߡ�GDC=��FDE=��ֵ����G�����ΪD���յ�ΪG�壬��ͼ2����ʾ��
���G���ƶ�·�����߶�DG�壮
�ߡ�G��DC=��BDA����DCG��=��A=90�㣬
���DCG��ס�DAB��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��DG��= ![]() ��
��
���G�ƶ�·�ߵij�Ϊ ![]() ��
��
����������1��ֻҪ֤�������ڽǵ���90�㼴�ɣ���2����֤��D�ڡ�O�ϣ�����Բ�ܽǶ����ɵá�FCE=��FDE���Ӷ�֤����CFE�ס�DAB���������������ε����ʿɵõ�S����EFCG=2S��CFE= ![]() ��Ȼ��ֻ�����CF�ķ�Χ�Ϳ����S����EFCG�ķ�Χ������Բ�ܽǶ����;��ε����ʿ�֤����GDC=��FDE=��ֵ���Ӷ��õ���G���ƶ���·�����߶Σ�ֻ���ҵ���G��������յ㣬������߶εij��ȼ��ɣ�
��Ȼ��ֻ�����CF�ķ�Χ�Ϳ����S����EFCG�ķ�Χ������Բ�ܽǶ����;��ε����ʿ�֤����GDC=��FDE=��ֵ���Ӷ��õ���G���ƶ���·�����߶Σ�ֻ���ҵ���G��������յ㣬������߶εij��ȼ��ɣ�

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�����Ŀ��ijУ������ȤС���ڱ�Уѧ���п�չ���ж��й�2013�������Ƚ��¼�֪�����ר���������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����ΪA��B��C��D���࣮���У�A���ʾ���dz��˽⡱��B���ʾ���Ƚ��˽⡱��C���ʾ�������˽⡱��D���ʾ����̫�˽⡱����������������������±���
��� | A | B | C | D |
Ƶ�� | 30 | 40 | 24 | b |
Ƶ�� | a | 0.4 | 0.24 | 0.06 |
��1�����е�a= �� b=��
��2�����ݱ������ݣ�������ͳ��ͼ�����ΪB��ѧ��������Ӧ������Բ�ĽǵĶ����� 
��3������У��ѧ��1000�������ݵ��������Ƹ�Уѧ�������ΪC������ԼΪ���٣�
����Ŀ���ס���������5�δ�в��������еĻ������£� �ף�8��8��7��8��9
�ң�5��9��7��10��9
��1��������
ƽ���� | ���� | ��λ�� | ���� | |
�� | 8 | 8 | 0.4 | |
�� | 9 | 3.2 |
��2������������5�γɼ���ѡ��ײμ����������������������ʲô��
��3������������1�Σ�����8������ô�ҵ�����ɼ��ķ��� �� ����������С�����䡱����
����Ŀ��Ϊ���˽�ij�г����꼶ѧ�������ɼ����ɼ���Ϊ�������������ȡ�˲���ѧ���������ɼ����ֶΣ�A��20.5��22.5��B��22.5��24.5��C��24.5��26.5��D��26.5��28.5��E��28.5��30.5��ͳ�����������ɼ�ͳ�Ʊ�
������ | Ƶ��/�� | Ƶ�� |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
���������ṩ����Ϣ���ش��������⣺
��1����ͳ�Ʊ��У�a= �� b= �� ����ͳ��ͼ���������� 
��2��С��˵�����������ݵ�����һ����C�У�������ΪС����˵����ȷ�������ȷ��������
��3�����ɼ���27�����ϣ���27�֣���Ϊ���㣬����н���48000�������꼶ѧ���������ɼ�Ϊ�����ѧ������Լ�ж��٣�