题目内容
【题目】如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（ ）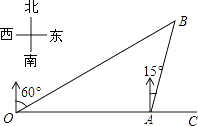
A.4km
B.2 
km
C.2 
km
D.（ +1）km
【答案】C
【解析】解：如图，过点A作AD⊥OB于D．
在Rt△AOD中，∵∠ADO=90°，∠AOD=30°，OA=4，
∴AD= 
OA=2．
在Rt△ABD中，∵∠ADB=90°，∠B=∠CAB﹣∠AOB=75°﹣30°=45°，
∴BD=AD=2，
∴AB= 
AD=2 ．
即该船航行的距离（即AB的长）为2 km．
故选：C．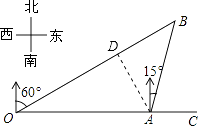
过点A作AD⊥OB于D．先解Rt△AOD，得出AD= OA=2，再由△ABD是等腰直角三角形，得出BD=AD=2，则AB= AD=2 ．
练习册系列答案
相关题目
【题目】为了了解某市初三年级学生体育成绩（成绩均为整数），随机抽取了部分学生的体育成绩并分段（A：20.5～22.5；B：22.5～24.5；C：24.5～26.5；D：26.5～28.5；E：28.5～30.5）统计如下体育成绩统计表
分数段 | 频数/人 | 频率 |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
根据上面提供的信息，回答下列问题：
（1）在统计表中，a= ， b= ， 并将统计图补充完整； 
（2）小明说：“这组数据的众数一定在C中．”你认为小明的说法正确吗？（填“正确”或“错误”）；
（3）若成绩在27分以上（含27分）定为优秀，则该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有多少？
