题目内容
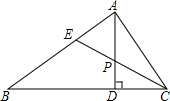
如图，△ABC中，AE⊥BC于E，AD是△ABC的角平分线，若∠ACB=40°，∠BAE=30°，则∠EAD=______度．
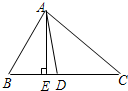
∵AE⊥BC于E，∠BAE=30°，
∴∠B=90°-∠BAE=90°-30°=60°，
∵∠ACB=40°，
∴∠BAC=180°-∠B-∠ACB=180°-60°-40°=80°，
∵AD是△ABC的角平分线，
∴∠BAD=
∠BAC=
×80°=40°，
∴∠EAD=∠BAC-∠BAE=40°-30°=10°．
故答案为：10．
∴∠B=90°-∠BAE=90°-30°=60°，
∵∠ACB=40°，
∴∠BAC=180°-∠B-∠ACB=180°-60°-40°=80°，
∵AD是△ABC的角平分线，
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EAD=∠BAC-∠BAE=40°-30°=10°．
故答案为：10．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
