题目内容
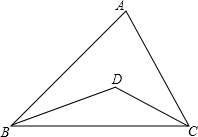
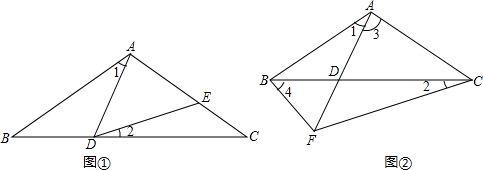
如图①,△ABC中,∠ABC=∠ACB,D是底边BC上的一点;
(1)在AC上取一点E,画△ADE,使∠ADE=∠AED=50°,∠2=20°,求∠1的度数;
(2)如图①,将题(1)中的条件“使∠ADE=∠AED=50°,∠2=20°”改为“∠ADE=∠AED”,试猜想:∠1与∠2的数量关系,并说明理由;
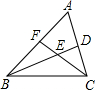
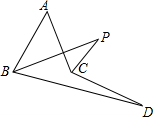
(3)如图②,延长AD到F,连结BF、FC,使∠ABF=∠AFB,∠AFC=∠ACF,试猜想:∠1与∠2、∠3与∠4之间的关系,并选其中一个进行证明.
(1)在AC上取一点E,画△ADE,使∠ADE=∠AED=50°,∠2=20°,求∠1的度数;
(2)如图①,将题(1)中的条件“使∠ADE=∠AED=50°,∠2=20°”改为“∠ADE=∠AED”,试猜想:∠1与∠2的数量关系,并说明理由;
(3)如图②,延长AD到F,连结BF、FC,使∠ABF=∠AFB,∠AFC=∠ACF,试猜想:∠1与∠2、∠3与∠4之间的关系,并选其中一个进行证明.

(1)∵∠AED=∠2+∠C,∠ADE=∠AED=50°,∠2=20°,
∴∠C=30°,∠DAC=180°-∠ADE-∠AED=80°,
∵∠ABC=∠ACB,
∴∠ABC=30°
∴∠BAC=180°-30°-30°=120°,
∴∠1=∠BAC-∠DAC=120°-80°=40°;
(2)∵∠2+∠ACB=∠AED,∠1+∠B=∠2+∠ADE,∠ADE=∠AED,
∴∠2+∠ACB=∠1+∠B-∠2,
∵∠B=∠ACB,
∴∠2=∠1-∠2,
∴∠1=2∠2;
(3)∠3=2∠4,∠1=2∠2,
证明:如图2,∵∠ACF+∠AFC+∠FAC=180°,∠ABC+∠ACB+∠BAC=180°,∠AFC=∠ACF,∠ABC=∠ACB,
∴∠ACF=
(180°-∠FAC)=90°-
∠3,∠ACB=
(180°-∠BAC)=90°-
(∠1+∠3),
∴∠2=∠ACF-∠ACB=(90°-
∠3)-(90°-
∠1-
∠3)=
∠1,
即∠1=2∠2.
∴∠C=30°,∠DAC=180°-∠ADE-∠AED=80°,
∵∠ABC=∠ACB,
∴∠ABC=30°
∴∠BAC=180°-30°-30°=120°,
∴∠1=∠BAC-∠DAC=120°-80°=40°;
(2)∵∠2+∠ACB=∠AED,∠1+∠B=∠2+∠ADE,∠ADE=∠AED,
∴∠2+∠ACB=∠1+∠B-∠2,
∵∠B=∠ACB,
∴∠2=∠1-∠2,
∴∠1=2∠2;
(3)∠3=2∠4,∠1=2∠2,
证明:如图2,∵∠ACF+∠AFC+∠FAC=180°,∠ABC+∠ACB+∠BAC=180°,∠AFC=∠ACF,∠ABC=∠ACB,
∴∠ACF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠2=∠ACF-∠ACB=(90°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠1=2∠2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,请填空:
,请填空: