题目内容
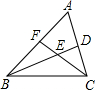
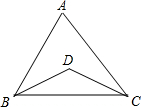
如图,AD,CE分别是△ABC的角平分线,它们的交点为F.若∠B=60°,∠ACB=72°,则∠BDA=______;若∠B=60°,∠BAC=48°,则∠DFC=______;若∠B=50°,则∠AFC=______.

∵AD,CE分别是△ABC的角平分线,∠B=60°,∠ACB=72°,
∴∠BAC=180°-60°-72°=48°,
∴∠BAD=
∠BAC=24°;
∵∠B=60°,∠BAC=48°,
∴∠ACB=180°-60°-48°=72°,
∵AD,CE分别是△ABC的角平分线,
∴∠BAD=
∠BAC=
×48°=24°,∠DCF=
∠ACB=
×72°=36°,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=60°+24°=84°,
∴∠DFC=180°-∠AC-∠DCE=180°-84°-36°=60°;
∴∠AFC=180°-∠DFC=180°-60°=120°.
故答案为:24°,60°,120°.
∴∠BAC=180°-60°-72°=48°,
∴∠BAD=
| 1 |
| 2 |
∵∠B=60°,∠BAC=48°,
∴∠ACB=180°-60°-48°=72°,
∵AD,CE分别是△ABC的角平分线,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=60°+24°=84°,
∴∠DFC=180°-∠AC-∠DCE=180°-84°-36°=60°;
∴∠AFC=180°-∠DFC=180°-60°=120°.
故答案为:24°,60°,120°.

练习册系列答案
相关题目
 ,请填空:
,请填空: