题目内容
如图,梯形ABCD中,AD∥BC,∠ABD=∠C,AB=2,AD=1.6,CD=3.
(1)求BD,BC的长;
(2)画出△BCD的外接圆(不写画法,保留作图痕迹),并指出AD是否为该圆的切线;
(3)计算tanC的值.

(1)求BD,BC的长;
(2)画出△BCD的外接圆(不写画法,保留作图痕迹),并指出AD是否为该圆的切线;
(3)计算tanC的值.

(1)∵AD∥BC,
∴∠ADB=∠DBC,
而∠ABD=∠C,
∴△ABD∽△DCB,
∴
=
=
,
∴
=
=
,
∴BD=2.4,BC=3.6.
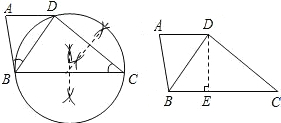
(2)△BCD的外接圆如右图所示,AD不是其外接圆的切线.
(3)方法一:
过D作DE⊥BC于E.
设CE=x,则BE=3.6-x.
根据勾股定理,得BD2-BE2=DE2=CD2-CE2,
即2.42-(3.6-x)2=DE2=32-x2,
解得x=
,DE=
.
∴在Rt△CDE中,有tanC=
=
.
方法二: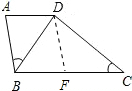
过D作DF∥AB交BC于F,则ABFD是平行四边形,
所以DF=2,CF=BC-BF=3.6-1.6=2,
∴△CDF是等腰三角形.
过F作FG⊥CD于G,则FG2=CF2-(
CD)2=
,FG=
,
∴在Rt△CFG中,有tanC=
=
.
∴∠ADB=∠DBC,
而∠ABD=∠C,
∴△ABD∽△DCB,
∴
| AB |
| DC |
| AD |
| BD |
| BD |
| BC |
∴
| 2 |
| 3 |
| 1.6 |
| BD |
| BD |
| BC |
∴BD=2.4,BC=3.6.
(2)△BCD的外接圆如右图所示,AD不是其外接圆的切线.
(3)方法一:
过D作DE⊥BC于E.
设CE=x,则BE=3.6-x.
根据勾股定理,得BD2-BE2=DE2=CD2-CE2,
即2.42-(3.6-x)2=DE2=32-x2,
解得x=
| 9 |
| 4 |
3
| ||
| 3 |
∴在Rt△CDE中,有tanC=
| DE |
| CE |
| ||
| 3 |
方法二:

过D作DF∥AB交BC于F,则ABFD是平行四边形,
所以DF=2,CF=BC-BF=3.6-1.6=2,
∴△CDF是等腰三角形.
过F作FG⊥CD于G,则FG2=CF2-(
| 1 |
| 2 |
| 7 |
| 4 |
| ||
| 2 |
∴在Rt△CFG中,有tanC=
| DE |
| CE |
| ||
| 3 |


练习册系列答案
相关题目




