题目内容
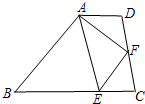
已知：如图，在梯形ABCD中，AB∥DC，中位线EF=7cm，对角线AC⊥BD，∠BDC=30°．求梯形的高AH．
过A作AM∥BD，交CD的延长线于M．
∵AB∥DC，
∴DM=AB，∠AMC=∠BDC=30°，
又∵中位线EF=7cm，
∴CM=CD+DM=CD+AB=2EF=14cm，
又∵AC⊥BD，
∴AC⊥AM，
∴AC=
CM=7cm．
∵AH⊥CD，∠ACD=60°，
∴AH=AC•sin60°=
cm．
∵AB∥DC，
∴DM=AB，∠AMC=∠BDC=30°，
又∵中位线EF=7cm，
∴CM=CD+DM=CD+AB=2EF=14cm，
又∵AC⊥BD，
∴AC⊥AM，
∴AC=
| 1 |
| 2 |
∵AH⊥CD，∠ACD=60°，
∴AH=AC•sin60°=
| 7 |
| 2 |
| 3 |
练习册系列答案
名校课堂系列答案
相关题目
