题目内容
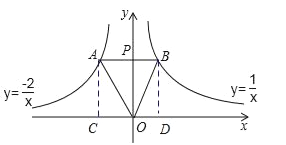
【题目】如图,点P是y轴正半轴上的一动点,过点P作AB∥x轴,分别交反比例函数![]() (x<0)与
(x<0)与![]() (x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.
(x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
解:设P的坐标为(0,b),b>0
过点A、B作AC⊥x轴于点C、BD⊥x轴于点D,令y=m分别代入![]() ,
,![]() ,∴A(
,∴A(![]() ,b),B(
,b),B(![]() ,b),∴AB=
,b),∴AB=![]() ,AP=
,AP=![]() ,BP=
,BP=![]() ,∴AP=2AB,故①正确;
,∴AP=2AB,故①正确;
tan∠AOP=![]() =
=![]() ,tan∠BOP=
,tan∠BOP=![]() =
=![]() ,∴tan∠AOP=2tan∠BOP,但∠AOP≠BOP,故②错误;
,∴tan∠AOP=2tan∠BOP,但∠AOP≠BOP,故②错误;
△ABO的面积为:![]() ABOP=
ABOP=![]() ×
×![]() ×b=
×b=![]() ,故③正确;
,故③正确;
由勾股定理可知:OA2=![]() +b2,OB2=b2+
+b2,OB2=b2+![]() ,∵AB2=
,∵AB2=![]() ,∴OA、OB、OA三边不一定相等,故④错误;
,∴OA、OB、OA三边不一定相等,故④错误;
故选B.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目



