题目内容
【题目】如图，小明想测山高和索道的长度．他在B处仰望山顶A，测得仰角∠B＝31°，再往山的方向(水平方向)前进80 m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE＝39°.
(1)求这座山的高度(小明的身高忽略不计)；
(2)求索道AC的长(结果精确到0.1 m)．
(参考数据：tan31°≈
，sin31°≈
，tan39°≈
，sin39°≈
)
【答案】（1）山的高度为180米；（2）索道AC长约为282.9米.
【解析】
试题（1）通过作垂线构造直角三角形，把已知角放到直角三角形中，设出未知数x,用x代数式表示出BD、CD，利用线段之差列出方程；
（2）在Rt△ACD中利用sin39°，由AD求出AC.
试题解析：（1）过点A作AD⊥BE于D，
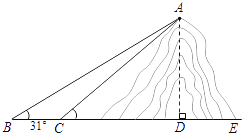
设山AD的高度为x米，
在Rt△ABD中，
∵∠ADB=90°，tan31°=
，
∴BD=
≈
=
x，
在Rt△ACD中，
∵∠ADC=90°，tan39°=
，
∴CD==
≈
=
x，
∵BC=BD﹣CD，
∴
=80，
解得：x=180，
即山的高度为180米；
（2）在Rt△ACD中，∠ADC=90°，
sin39°=
，
∴AC=
= 
≈282.9（m），
答：索道AC长约为282.9米．
【题目】汽车租赁公司拥有某种型号的汽车100辆．公司在经营中发现每辆车的月租金x（元）与每月租出的车辆数（y）有如下关系：
x（元） | 3000 | 3200 | 3500 | 4000 |
y（辆） | 100 | 96 | 90 | 80 |
（1）观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求按照表格呈现的规律，每月租出的车辆数y（辆）与每辆车的月租金x（元）之间的关系式．
（2）已知租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．用含x（x≥3000）的代数式填表：
租出的车辆数（辆） | ________ | 未租出的车辆数（辆） | ________ |
租出每辆车的月收益（元） | ________ | 所有未租出的车辆每月的维护费（元） | ________ |
（3）若你是该公司的经理，你会将每辆车的月租金定为多少元，才能使公司获得最大月收益？请说明理由．
